Hierarchie de Borel

Hierarchie de Borel: Hiérarchie de Borel

Définition des ensembles de Borel

Une algèbre sur un ensemble $X$ est une collection 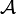$\mathcal{A}$ de sous-ensembles de $X$ vérifiant les conditions suivantes: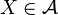

$X\in \mathcal{A}$

Si 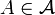$A\in \mathcal{A}$ , alors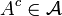 $A^c\in \mathcal{A}$

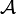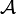Toute union finie d'éléments de $\mathcal{A}$ appartient à $\mathcal{A}$ .

Remarquer que 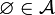$\varnothing \in \mathcal{A}$ pour toute algèbre 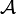$\mathcal{A}$ . Une algèbre 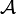$\mathcal{A}$ telle que toute union dénombrable d'éléments de 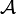$\mathcal{A}$ appartient à 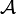$\mathcal{A}$ est appelée une $σ$ -algèbre.

Il est facile de voir que l'intersection d'une famille non-vide de $σ$ -algèbres sur $X$ est une $σ$ -algèbre. Cette constatation permet la définition suivante. Soit 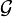$\mathcal{G}$ une famille de sous-ensembles de $X$ . Soit 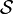$\mathcal{S}$ l'ensemble des $σ$ -algèbres sur $X$ contenant 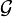$\mathcal{G}$ . Noter que 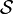$\mathcal{S}$ est non-vide car la $σ$ -algèbre 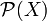$\mathcal{P}(X)$ contient trivialement 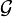$\mathcal{G}$ . 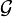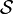On appelle $σ$ -algèbre engendrée par $\mathcal{G}$ l'intersection de tous les membres de $\mathcal{S}$ .

Soit 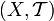$(X,\mathcal{T})$ un espace topologique métrisable. On appelle $σ$ -algèbre des noréliens sur X la $σ$ -algèbre engendrée par 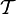$\mathcal{T}$ . Elle est notée 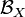$\mathcal{B}_X$ . Un membre de la $σ$ -algèbre des boréliens est appelé un borélien ou ensemble de Borel.

Hiérarchie des boréliens

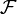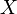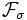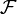Soit $\mathcal{F}$ une famille de sous-ensembles d'un ensemble $\quad X$ . On note $\mathcal{F}_{\sigma}$ l'ensemble des unions dénombrables d'éléments de $\mathcal{F}$ :

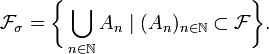
$\mathcal{F}_{\sigma} = \bigg\{ \bigcup_{n\in \N} A_n \mid (A_n)_{n\in \N} \subset \mathcal{F}\bigg\}.$

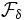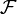On note également par $\mathcal{F}_{\delta}$ l'ensemble des intersections dénombrables de $\mathcal{F}$ :

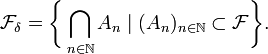
$\mathcal{F}_{\delta} = \bigg\{\bigcap_{n\in \N} A_n \mid (A_n)_{n\in \N} \subset \mathcal{F}\bigg\}.$

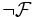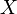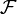On désigne finalement par $\neg \mathcal{F}$ l'ensemble des compléments dans $\quad X$ des éléments de $\mathcal{F}$ :

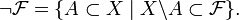
$\neg \mathcal{F} = \{ A\subset X \mid X\backslash A \subset \mathcal{F} \}.$

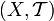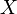Soit un espace topologique $(X,\mathcal{T})$ . Notons de la manière suivante les ouverts et les fermés de $\quad X$ :

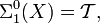
$\Sigma_1^0(X)=\mathcal{T},$

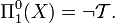
$\Pi_1^0(X)=\neg \mathcal{T}.$

Puis pour chaque ordinal $α$ , $1 < α < ω 1$ , on définit alors les familles d'ensembles suivants par induction transfinie:

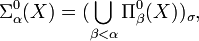
$\Sigma_{\alpha}^0(X)=(\bigcup_{\beta<\alpha} \Pi_{\beta}^0(X))_{\sigma},$

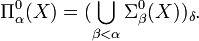
$\Pi_{\alpha}^0(X)=(\bigcup_{\beta<\alpha} \Sigma_{\beta}^0(X))_{\delta}.$

Finalement pour chaque ordinal $α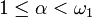$ , $1 \leq \alpha < \omega_1$ , on définit: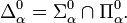

$\Delta_{\alpha}^0 = \Sigma_{\alpha}^0 \cap \Pi_{\alpha}^0.$

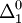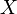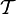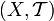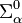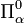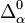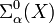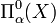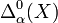Notons que $\Delta_{1}^0$ est la famille des ensembles de $\quad X$ qui sont à la fois ouverts et fermés pour la topologie $\mathcal{T}$ . S'il n'y a pas d'ambiguïté, ou si un résultat est valable pour tout espace topologique $(X,\mathcal{T})$ , on note parfois $\Sigma_{\alpha}^0$ , $\Pi_{\alpha}^0$ et $\Delta_{\alpha}^0$ au lieu de $\Sigma_{\alpha}^0(X)$ , $\Pi_{\alpha}^0(X)$ et $\Delta_{\alpha}^0(X)$ . 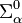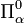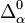Les familles $\Sigma_{\alpha}^0$ , $\Pi_{\alpha}^0$ et $\Delta_{\alpha}^0$ sont appelées les classes additives, multiplicatives et ambiguës. Ces familles d'ensembles vérifient les propriétés élémentaires suivantes.

Les classes additives sont closes par unions dénombrables, et les classes multiplicatives sont closes par intersections dénombrables.

Pour tout ordinal $α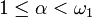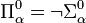$ , $1\leq \alpha < \omega_1$ , $\Pi_{\alpha}^0 = \neg \Sigma_{\alpha}^0$ , ou de manière équivalente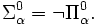 $\Sigma_{\alpha}^0 = \neg \Pi_{\alpha}^0.$

Pour tout ordinal $α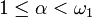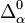$ , $1\leq \alpha < \omega_1$ , $\Delta_{\alpha}^0$ est une algèbre.

On montre alors que:

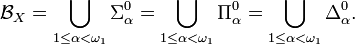
$\mathcal{B}_X = \bigcup_{1\leq \alpha < \omega_1} \Sigma_{\alpha}^0 = \bigcup_{1\leq \alpha < \omega_1} \Pi_{\alpha}^0 = \bigcup_{1\leq \alpha < \omega_1} \Delta_{\alpha}^0 .$

Notes et références

tribu borélienne

S.M. Srivastava, A course on Borel sets, Springer, 1991

Portail des mathématiques

Ce document provient de « Hi%C3%A9rarchie de Borel ».

Catégorie : Théorie des ensembles

Contenu soumis à la licence CC-BY-SA. Source : Article Hierarchie de Borel de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Hiérarchie De Borel — Définition des ensembles de Borel Une algèbre sur un ensemble X est une collection de sous ensembles de X vérifiant les conditions suivantes: Si , alors Toute union finie d … Wikipédia en Français
Hiérarchie de borel — Définition des ensembles de Borel Une algèbre sur un ensemble X est une collection de sous ensembles de X vérifiant les conditions suivantes: Si , alors Toute union finie d … Wikipédia en Français
Hiérarchie de Borel — La hiérarchie de Borel désigne une description de la tribu des boréliens d un espace topologique X comme une réunion croissante d ensembles de parties de X, indexée par le premier ordinal non dénombrable. Sommaire 1 Notations préliminaires 2… … Wikipédia en Français
Hiérarchie arithmétique — En logique mathématique, plus particulièrement en théorie de la calculabilité, la hiérarchie arithmétique, définie par Kleene est une hiérarchie des sous ensembles de l ensemble N des entiers naturels définissables dans le langage du premier… … Wikipédia en Français
Hierarchie mathematischer Strukturen — Dieser Artikel gibt einen Überblick über die Hierarchie mathematischer Strukturen. Unter einer mathematischen Struktur wird hier eine Menge verstanden, die mit bestimmten Eigenschaften ausgestattet ist. Algebraische Strukturen sind mit einer oder … Deutsch Wikipedia
Algèbre de Borel — Tribu borélienne La tribu borélienne sur un (ou d un) espace topologique T est la plus petite σ algèbre sur T contenant tous les ensembles ouverts. Les éléments de la tribu borélienne sont appelés des boréliens. La tribu de Borel peut, de manière … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Tribu engendrée — Étant donné un ensemble de parties d un même ensemble X, la tribu engendrée par est la plus petite tribu (au sens de l inclusion) contenant . On la note . Sommaire 1 D … Wikipédia en Français
Théorie descriptive des ensembles — La théorie descriptive des ensembles est une branche des mathématiques s intéressant aux ensembles « définissables ». Son principal but est de classifier ces ensembles par complexité. Elle a de nombreux liens avec la théorie des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Hierarchie de Borel

Hiérarchie de Borel

Définition des ensembles de Borel

Hiérarchie des boréliens

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Hierarchie de Borel

Hiérarchie de Borel

Définition des ensembles de Borel

Hiérarchie des boréliens

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link