Géodésie physique (verticale et surface de niveau)

Géodésie physique (verticale et surface de niveau)

Verticale et surface de niveau

Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu'il est représenté sur un plan. La verticale d'un point de la surface est une ligne imaginaire traversant ce point et dirigé vers le bas, suivant la pesanteur. Les surfaces de niveau sont les tracés formés sur la surface par son intersection avec des plans perpendiculaires à la verticale et espacés à des altitudes régulières.

Sommaire

Verticale et pesanteur

La verticale, en un lieu repéré par un point P sur la surface terrestre ou dans son voisinage, est définie par la direction de la pesanteur 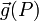\vec g (P) en P, et matérialisée par la direction d'un fil à plomb suspendu en P ou par l'axe « vertical » d'un niveau optique mise en station au point P. La pesanteur s'obtient en prenant le gradient du potentiel de pesanteur U(P), somme des potentiels gravifique V(P) et axifuge Z(P), au point P. 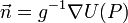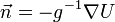Selon qu'on décide par convention d'orienter la verticale vers l'intérieur de la Terre ou vers l'extérieur, le vecteur unitaire fournissant l'orientation de la verticale du lieu est fourni par \vec n = g^{-1} \nabla U(P) ou \vec n = - g^{-1} \nabla U, respectivement. 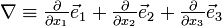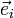Le symbole \nabla (nabla) désigne l'opérateur gradient, qui en coordonnées cartésiennes (x1,x2,x3) peut s'écrire \nabla \equiv \tfrac{\partial}{\partial x_1} \vec e_1 + \tfrac{\partial}{\partial x_2} \vec e_2 + \tfrac{\partial}{\partial x_3} \vec e_3, \vec e_i désignant un vecteur unitaire orienté positivement le long de l'axe Oxi.

Gradient du potentiel de pesanteur et dérivée dans une direction

Le gradient du champ scalaire U est un champ vectoriel, en l'occurrence le champ de pesanteur 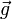\vec g. Le potentiel de pesanteur U étant une fonction du point P, le voisinage de P peut être décrit par un petit vecteur 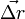\vec{\Delta r} joignant P à tout point voisin Q. Le taux de croissance de la fonction U sera en général différent selon la direction et le sens de 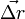\vec{\Delta r}, et nous pouvons écrire comme suit le taux de croissance de U(P) dans la direction caractérisée par le vecteur unitaire 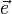\vec e :[1]

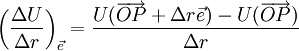
\left(\frac{\Delta U}{\Delta r}\right)_{\vec e} = \frac{U(\overrightarrow{OP} + \Delta r \vec e) - U(\overrightarrow{OP})}{\Delta r}

et définir la dérivée du potentiel de pesanteur U(P) dans la direction du vecteur unitaire 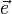\vec e pa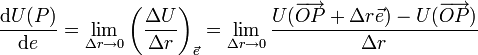r

\frac{\mathrm{d}U(P)}{\mathrm{d}e} = \lim_{\Delta r \rightarrow 0} \left(\frac{\Delta U}{\Delta r}\right)_{\vec e} = \lim_{\Delta r \rightarrow 0} \frac{U(\overrightarrow{OP} + \Delta r \vec e) - U(\overrightarrow{OP})}{\Delta r}.

Lorsque le vecteur unitaire 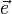\vec e possède la direction et le sens d'un axe du trièdre de référence, soit Oxi orienté selon le vecteur unitaire 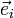\vec e_i, ceci permet de définir les dérivées partielles

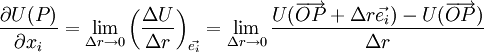\frac{\partial U(P)}{\partial x_i} = \lim_{\Delta r \rightarrow 0} \left(\frac{\Delta U}{\Delta r}\right)_{\vec {e_i}} = \lim_{\Delta r \rightarrow 0} \frac{U(\overrightarrow{OP} + \Delta r \vec {e_i}) - U(\overrightarrow{OP})}{\Delta r}.

Constatons toutefois que ces dérivées partielles ne sont pas très intéressantes car elles dépendent manifestement du choix du système de référence et ne sont donc pas des quantités scalaires. Par contre, les dérivées dans une direction représentent des fonctions scalaires, le système de référence n'intervenant pas dans leur définition.

On démontre en analyse mathématique, par exemple en se basant sur la formule des accroissements finis, que

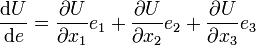\frac{\mathrm{d}U}{\mathrm{d}e} = \frac{\partial U}{\partial x_1} e_1 + \frac{\partial U}{\partial x_2} e_2 + \frac{\partial U}{\partial x_3} e_3,

où e1, e2, e3 sont les composantes du vecteur unitaire 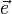\vec e ou encore, ce qui est équivalent, les cosinus directeurs de l'axe dans la direction duquel on dérive. Cette dernière formule indique que la dérivée de U dans la direction du vecteur unitaire 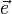\vec e s'obtient en formant un produit scalaire, à savoir

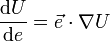\frac{\mathrm{d}U}{\mathrm{d}e} = \vec{e} \cdot \nabla U.

Surface de niveau

Article connexe : Ligne de niveau.

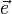La formule précédente a des conséquences fort intéressantes. En effet, si \varphi désigne l'angle entre la direction du gradient du potentiel de pesanteur U (donc la direction de la verticale) et la direction \vec e, la dérivée 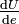\tfrac{\mathrm{d}U}{\mathrm{d}e} du potentiel de pesanteur le long de 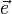\vec e peut s'écrire

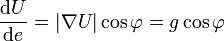\frac{\mathrm{d}U}{\mathrm{d}e} = |\nabla U| \cos{\varphi} = g \cos{\varphi}.

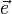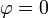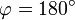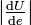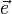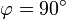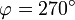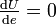Ainsi, si \vec e est parallèle à la direction de la verticale en P (c'est-à-dire \varphi = 0 ou \varphi = 180^\circ), \left|\tfrac{\mathrm{d}U}{\mathrm{d}e}\right| est maximum et vaut g, et si \vec e est perpendiculaire à la verticale en P (c'est-à-dire \varphi = 90^\circ ou \varphi = 270^\circ), \tfrac{\mathrm{d}U}{\mathrm{d}e} = 0. En d'autres termes, le taux de variation du potentiel de pesanteur est maximum en valeur absolue dans la direction de la verticale, et nul dans une direction contenue dans le plan perpendiculaire à la verticale en P. Ce plan est donc tangent en P à la surface

U(P) = constante

qu'on appelle surface de niveau. Pour un point arbitraire, la pesanteur 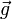\vec g, autrement dit le gradient du potentiel de pesanteur U, est donc normale à la surface de niveau passant par ce point. Comme le potentiel de pesanteur reste constant sur une surface de niveau, on parle aussi d'une surface équipotentielle du champ de pesanteur.

Liens internes

Liens externes

Notes

  1. ↑ Le point P appartient à un espace de points ; son analogue dans l'espace vectoriel associé est 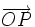\overrightarrow{OP}, le point O étant un point arbitraire de l'espace ponctuel considéré comme point-origine.
  • Portail de la géodésie et de la géophysique Portail de la géodésie et de la géophysique
  • Portail de l’astronomie Portail de l’astronomie
  • Portail de la géographie Portail de la géographie
  • Portail de la physique Portail de la physique
Ce document provient de « Verticale et surface de niveau ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Géodésie physique (verticale et surface de niveau) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Géodésie physique (verticale en un lieu) — Verticale et surface de niveau Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu il est représenté sur un plan. La verticale d un point de la surface est une ligne imaginaire… …   Wikipédia en Français

  • Verticale et surface de niveau — Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu il est représenté sur un plan. La verticale d un point de la surface est une ligne imaginaire traversant ce point et dirigé vers le …   Wikipédia en Français

  • Surface de niveau — Verticale et surface de niveau Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu il est représenté sur un plan. La verticale d un point de la surface est une ligne imaginaire… …   Wikipédia en Français

  • Géodésie physique (pesanteur et gravité) — Pesanteur  Ne doit pas être confondu avec apesanteur. Schéma montrant la vitesse d un objet en fonction du temps lorsqu i …   Wikipédia en Français

  • Verticale en un lieu — Verticale et surface de niveau Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu il est représenté sur un plan. La verticale d un point de la surface est une ligne imaginaire… …   Wikipédia en Français

  • Pesanteur et gravité (Géodésie physique) — Pesanteur  Ne doit pas être confondu avec apesanteur. Schéma montrant la vitesse d un objet en fonction du temps lorsqu i …   Wikipédia en Français

  • Pesanteur et gravité (géodésie physique) — Pesanteur  Ne doit pas être confondu avec apesanteur. Schéma montrant la vitesse d un objet en fonction du temps lorsqu i …   Wikipédia en Français

  • GÉODÉSIE — La géodésie (du grec 塚兀, la terre ; 嗀見晴﨎晴益, diviser) s’est développée à partir des méthodes d’arpentage, nécessaires pour la délimitation précise des propriétés rurales, dès la plus haute antiquité. La compétence des opérateurs s’est… …   Encyclopédie Universelle

  • Geodesie — Géodésie La géodésie tire son nom des mots grecs γη (Terre) et δαιω (je divise). Cette science, à l’origine destinée au tracé des cartes, s’est ensuite attachée à résoudre le problème des dimensions, puis de la forme de la planète Terre. Selon la …   Wikipédia en Français

  • niveau — [ nivo ] n. m. • nivel 1311; altér. de livel XIIIe (cf. angl. level), lat. pop. °libellus, class. libella I ♦ Instrument qui sert à donner l horizontale, à vérifier l horizontalité. Niveau d eau : instrument à deux vases communicants qui, remplis …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”