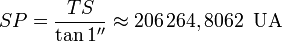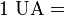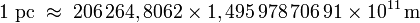Gigaparsec

Le parsec (symbole pc) est une unité de longueur utilisée en astronomie. Son nom vient de la contraction de « parallaxe-seconde ».

Cette unité résulte de l’utilisation d’une méthode trigonométrique dite « méthode de la parallaxe », servant à déterminer la distance séparant un observateur d’un objet éloigné quelconque, à la mesure de la distance des objets célestes.

Sommaire 1 Définition 2 Calcul de la valeur d'un parsec 3 Approximations utiles 3.1 Articles connexes 3.2 Liens externes

Définition

Le parsec est défini comme étant la distance à laquelle une unité astronomique (ua) sous-tend un angle d’une seconde d'arc. Si la parallaxe d’une étoile est mesurée en secondes d’arc, alors la distance entre cette étoile et le Soleil, exprimée en parsecs, est égale à l’inverse de cette valeur.

Comme le montre le calcul ci-dessous, un parsec vaut 3,085 677×10¹⁶ m, soit environ 3,261 564 années-lumière.

Pour des raisons pratiques, les astronomes expriment souvent les distances des objets astronomiques en parsecs plutôt qu’en années-lumière.

Les premières mesures de distance interstellaire (l’étoile 61 Cygni par Friedrich Wilhelm Bessel en 1838) furent effectuées en utilisant la largeur de l’orbite terrestre comme référence. Le parsec dériva de cette méthode. La détermination des distances des corps célestes est l’objet principal de l’astrométrie.

L’étoile la plus proche du Soleil, α Cen C (Proxima Centauri), se trouve à 1,316 parsec (4,28 années-lumière). Les distances des autres objets célestes n’appartenant pas au système solaire sont bien plus grandes et se mesurent couramment en kiloparsecs (symbole kpc) ou mégaparsecs (symbole Mpc).

Les parallaxes ont des valeurs faibles : 0,76″ pour Proxima Centauri ; aussi, la méthode parallactique ne permet guère de déterminer des distances stellaires supérieures à 100 parsecs environ, ce qui correspond à des mesures de parallaxe inférieures à 10 millisecondes d’arc.

Entre 1989 et 1993, le satellite Hipparcos, lancé par l’Agence spatiale européenne, a mesuré la parallaxe d’environ 100 000 étoiles avec une précision supérieure à la milliseconde d’arc, ce qui a permis de déterminer la distance d’étoiles éloignées de nous de plus d’un kiloparsec.

Calcul de la valeur d'un parsec

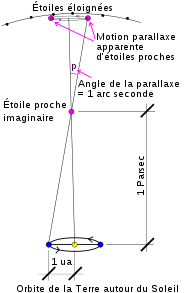
Sur le schéma ci-contre (d’échelle très réduite et ne respectant pas les valeurs angulaires), S est le Soleil, T la Terre et P un objet situé à un parsec du Soleil : par définition, l’angle 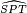est égal à une seconde d’arc (1″) et la distance [TS] vaut une unité astronomique (1 UA). Grâce aux règles de trigonométrie, il est possible de calculer [SP] :

Comme

on a

et

Le choix d'une définition arbitraire, mais très précise, de l'unité astronomique explique la précision des valeurs précédentes, qui pourrait surprendre a priori, et est toute théorique ; les mesures astronomiques, en particulier celles des parallaxes, étant en pratique bien rarement meilleures qu'à 1% près.

Approximations utiles

Sur le schéma ci-dessus, l'angle censé être d'une seconde a une valeur bien supérieure, et par conséquent l'hypoténuse est clairement plus longue que le côté adjacent. En réalité, pour un angle aussi petit, la différence de longueur entre les deux est très faible en valeur relative, et finalement l'hypoténuse vaut à peine plus d'un parsec (autrement dit, un parsec est aussi bien la distance du Soleil à l'étoile lointaine que de la Terre à l'étoile lointaine).

Il faut également se souvenir que pour les très faibles valeurs d'angles, on peut faire l'approximation (développement limité au premier ordre) 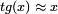(et de même 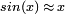, d'où l'affirmation suivant laquelle le côté adjacent et l'hypoténuse sont quasiment égaux), x étant l'angle exprimé en radians, qui vaut ici  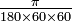; l'erreur relative commise étant (en radians) de l'ordre de x², donc ici, pour des longueurs de l'ordre d'un parsec, on commet (en utilisant ces formules) une erreur de l'ordre de la distance Terre-Lune, ce qui peut sembler important, mais est évidemment négligeable aux échelles astronomiques considérées.

Articles connexes

• Année-lumière
• Table des constantes astrophysiques
• Unité astronomique

Liens externes

• Conversion de parsec vers autres unités de longueur

• Portail de l’astronomie