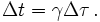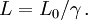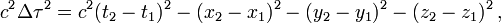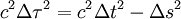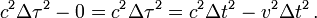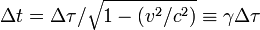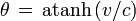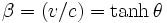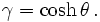Il est défini par : 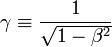$\gamma \equiv \frac{1}{\sqrt{1 - \beta^2}}$ où $β = v / c$ est le rapport de la vitesse v du mobile considéré à la vitesse de la lumière.

Sommaire

1 Quelques valeurs
2 Principale utilisation
3 Démonstration
4 Remarque
5 Voir aussi

Quelques valeurs

La table suivante indique quelques valeurs du facteur de Lorentz correspondant à différentes valeurs de la vitesse, données en pourcentage de c.

%c	γ	1/γ
0	1.000	1.000
10	1.005	0.995
50	1.155	0.867
90	2.294	0.436
99	7.089	0.141
99.9	22.366	0.045

Pour une vitesse v égale à la vitesse de la lumière à 10^-8 près, γ vaudra 0,7×10⁴.

voir aussi
Dilatation du temps des rayons cosmiques et des muons

Principale utilisation

Le facteur de Lorentz s'applique à la dilatation du temps et la contraction des longueurs en relativité restreinte.

On peut décrire ces effets en considérant les expériences imaginaires suivantes (imaginaires car pour que l'effet soit mesurable il est nécessaire que les vitesses soient proches de celle de la lumière).

Des observateurs terrestres situés le long du trajet d'une fusée donnée et observant son horloge à travers le hublot verront cette dernière tourner moins vite. Si Δτ est l'intervalle de temps lu sur l'horloge de la fusée, il lui correspondra pour les observateurs terrestres un temps Δt plus long donné par la formule

$\,\Delta t = \gamma \Delta\tau \,.$

Cette dilatation du temps est à l'origine du fameux paradoxe des jumeaux.

La contraction des longueurs est illustrée par le paradoxe du train. Si un train de longueur propre L₀ (c'est la longueur mesurée par un observateur au repos par rapport au train) passe dans un tunnel de même longueur propre L₀, les observateurs situés sur la voie pourront constater qu'à un instant donné pour eux le train semble plus court que le tunnel, sa longueur en quelque sorte « apparente » L étant plus courte que le tunnel et donnée par la formule

$\,L=L_0/\gamma \,.$

Démonstration

La relativité restreinte raisonne sur des événements repérés dans un espace-temps à quatre dimensions par une coordonnée temporelle t et trois coordonnées spatiales (x, y, z). Si on considère deux événements E1 et E2 de coordonnées (t₁, x₁, y₁, z₁) et (t₂, x₂, y₂, z₂) on définit le carré de l'intervalle d'espace-temps Δτ entre ces deux événements par la formule

$\,c^2\Delta\tau^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 \,,$

$\,c^2\Delta\tau^2 = c^2\Delta t^2 - \Delta s^2$

si Δt et Δs représentent la distance temporelle et la distance spatiale entre les deux événements.

Le relativité restreinte pose que cette quantité est indépendante du repère dans lequel elle est calculée. Elle est dite invariante par changement de coordonnées.

Appliquons cette propriété d'invariance à deux événements se produisant dans la fusée. Considérons ainsi deux éclairs successifs séparés par un intervalle de temps Δτ mesuré dans la fusée (il suffit de lire l'heure indiquée par l'horloge embarquée). Dans le repère fixe, les deux observateurs terrestres en coïncidence avec les éclairs 1 et 2 notent l'heure sur leur horloge et mesurent une différence de temps égale à Δt. Ces deux observateurs terrestres sont situés à une distance égale à v Δt si v est la vitesse de la fusée. Cette quantité représente la distance spatiale entre les événements E1 et E2 dans le repère fixe. Comme les deux éclairs sont émis dans la fusée, la distance spatiale entre ces deux mêmes événements évaluée dans le repère de la fusée est nulle. En écrivant l'invariance de la quantité c²Δt² - Δs² on obtient

$\,c^2\Delta\tau^2 - 0 = c^2\Delta\tau^2 = c^2\Delta t^2 - v^2\Delta t^2\,.$

Cette formule redonne bien

$\Delta t = \Delta\tau/\sqrt{1 - (v^2/c^2)}\equiv \gamma\Delta\tau$

Remarque

En introduisant le paramètre angulaire de vitesse θ défini par la formule

$\theta \,=\, \mathrm{atanh} \,(v/c)$

on a

$\,\beta = (v/c) = \tanh \theta$

$\,\gamma = \cosh\theta\,.$

Ce changement de variable permet d'écrire plus simplement les formules de Lorentz.

Voir aussi

Portail de la physique

Ce document provient de « Facteur de Lorentz ».

Catégorie : Relativité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Gamma relativiste de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Relativiste — Ne doit pas être confondu avec relativisme. En physique, le qualificatif de relativiste appliqué à un objet, signifie que cet objet est animé d une vitesse non négligeable par rapport à la vitesse de la lumière. Dans le cas contraire on… … Wikipédia en Français
Non-relativiste — Relativiste Ne doit pas être confondu avec relativisme … Wikipédia en Français
Non relativiste — Relativiste Ne doit pas être confondu avec relativisme … Wikipédia en Français
Mécanique relativiste — Principe de relativité Pour les articles homonymes, voir relativité … Wikipédia en Français
Sursaut gamma — Ne pas confondre avec sursauteur gamma mou, phénomène moins énergétique mais récurrent. Sursaut gamma GRB990123, image prise par le télescope spatial Hubble, le 23 … Wikipédia en Français
Gaz parfait relativiste — Le gaz parfait relativiste est un modèle de théorie cinétique des gaz qui considère un gaz composé de particules relativistes n interagissant pas entre elles. Contrairement au gaz parfait « classique » qu il généralise, il prend en… … Wikipédia en Français
Voyage relativiste — En astronautique, un voyage relativiste est un voyage interstellaire dans lequel on essaye d exploiter les effets relativistes de dilatation du temps pour franchir, en principe, des distances arbitrairement grandes dans un laps de temps local au… … Wikipédia en Français
Quantite de mouvement — Quantité de mouvement En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et à la masse d un objet. Elle fait partie, avec l énergie, des valeurs qui se conservent lors des interactions entre éléments du système.… … Wikipédia en Français
Quantité de mouvement — En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et à la masse d un objet. Elle fait partie, avec l énergie, des grandeurs qui se conservent lors des interactions entre éléments du système. Cette loi, d abord… … Wikipédia en Français
Calculs Relativistes — Cet article se veut volontairement calculatoire pour montrer que l essentiel peut se déduire par le calcul des transformations de Lorentz. Cet article de physique fait partie de la série relativité … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Gamma relativiste

Facteur de Lorentz

Sommaire

Quelques valeurs

Principale utilisation

Démonstration

Remarque

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Gamma relativiste

Facteur de Lorentz

Sommaire

Quelques valeurs

Principale utilisation

Démonstration

Remarque

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link