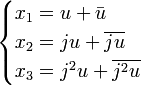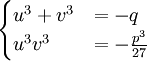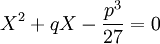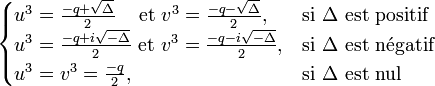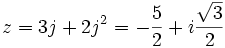- Formules de Cardan
-
Méthode de Cardan
La méthode de Cardan, proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545, est une méthode permettant de résoudre toutes les équations du troisième degré.
Cette méthode permet de mettre en place des formules appelées formules de Cardan donnant en fonction de p et q les solutions de l'équation :
Elle permet de prouver que les équations de degré 3 sont résolubles par radicaux. On rappelle que seules les équations de degré 1, 2, 3, 4 sont génériquement résolubles par radicaux, c’est-à-dire que seules ces équations possèdent des méthodes générales de résolutions donnant les solutions en fonction des coefficients du polynôme en utilisant seulement les quatre opérations habituelles sur les nombres rationnels, et l'extraction de racines carrées, cubiques et quartiques.
Sommaire
Formules de Cardan
Considérons l'équation
On calcule le discriminant
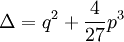 et on étudie son signe.
et on étudie son signe.(Remarque : Il existe aussi la notion de "discriminant écriture réduite" en posant p = 3p' , q = 2q' et
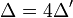 ; cela s'écrit
; cela s'écrit 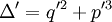 )
)Si l'on part de l'équation générale
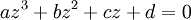 , on se ramène à la forme réduite en posant
, on se ramène à la forme réduite en posant 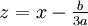 ,
, 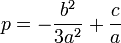 et
et  .
.Dans ce qui suit, on suppose p et q réels - bien que la méthode soit valable aussi s'ils sont complexes.
Si Δ est positif
L'équation possède alors une solution réelle et deux complexes. On pose
La seule solution réelle est alors
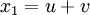 . Il existe également deux solutions complexes conjuguées l'une de l'autre
. Il existe également deux solutions complexes conjuguées l'une de l'autre 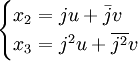 où
où 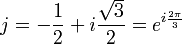 .
.Si Δ est nul
L'équation possède alors deux solutions réelles, une simple et une double :
Si Δ est négatif
L'équation possède alors trois solutions réelles. Toutefois, il est nécessaire de faire une incursion dans les complexes pour toutes les trouver (voir remarque historique). Les solutions sont les sommes de deux complexes conjugués
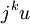 et
et 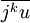 où
où ![u=\sqrt[3]{\frac{-q + i\sqrt{-\Delta}}{2}}](/pictures/frwiki/50/2e86db500e5c6bc0684f441cf634a44d.png) et
et 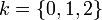 , soit l'ensemble suivant :
, soit l'ensemble suivant :La forme réelle des solutions est obtenue en écrivant jku sous la forme trigonométrique, ce qui donne :
Principe de la méthode
Considérons l'équation générale du troisième degré suivante :
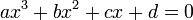 .
.En posant
 , on se ramène à une équation de la forme :
, on se ramène à une équation de la forme : 
où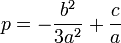 et
et  .
.On va maintenant poser
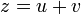 avec u et v complexes, de façon à avoir deux inconnues au lieu d'une et se donner ainsi la possibilité de poser ultérieurement une condition sur u et v permettant de simplifier le problème. L'équation
avec u et v complexes, de façon à avoir deux inconnues au lieu d'une et se donner ainsi la possibilité de poser ultérieurement une condition sur u et v permettant de simplifier le problème. L'équation  devient ainsi
devient ainsi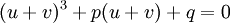 .
.
Cette équation se transforme aisément sous la forme suivante :
La condition de simplification annoncée sera alors
 . Ce qui nous donne d'une part
. Ce qui nous donne d'une part 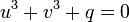 et d'autre part
et d'autre part 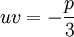 , qui, en élevant les deux membres à la puissance 3 donne
, qui, en élevant les deux membres à la puissance 3 donne 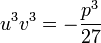 .
.Nous obtenons finalement le système somme-produit des deux inconnues u3 et v3 suivant :
Les inconnues u3 et v3 étant deux complexes dont on connaît la somme et le produit, ils sont donc les solutions de l'équation du second degré :
Le discriminant de cette équation est
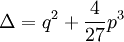 et les racines sont
et les racines sontIl suffit alors d'associer les trois racines cubiques de u3 et v3 deux par deux de façon à obtenir trois couples (u,v) tel que
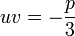 , puis reporter les trois couples de valeurs trouvés pour u et v dans l'expression
, puis reporter les trois couples de valeurs trouvés pour u et v dans l'expression 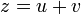 .
.Enfin, on revient au premier changement de variable
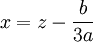 pour avoir les trois racines de l'équation du troisième degré posée au départ.
pour avoir les trois racines de l'équation du troisième degré posée au départ.Exemples
Exemple 1
Considérons par exemple l'équation
 ou encore
ou encore  . On a
. On a  et
et 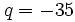 , donc :
, donc : 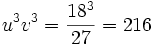 et
et 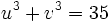 donc
donc 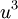 et
et  sont racines de l'équation
sont racines de l'équation  , dont les racines sont 27 et 8. Donc u et v valent 3 et 2 et la solution cherchée est
, dont les racines sont 27 et 8. Donc u et v valent 3 et 2 et la solution cherchée est  .
.Si on se place dans
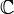 , alors les autres racines sont
, alors les autres racines sont 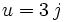 et
et 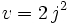 , où
, où 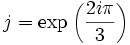 , ou bien
, ou bien 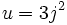 et
et 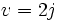 . On obtient donc comme autres racines :
. On obtient donc comme autres racines :Remarquons qu'avant de se lancer dans de tels calculs, il vaut mieux « tester » un peu le résultat à l'aide de la règle de Wheeler. Un graphique donne déjà la règle de Descartes : il n'y aura qu'une racine réelle ; elle est comprise entre 4 et 6. Et 53 = 125 et
 donc 5 est racine.
donc 5 est racine.Le reste en découle : P(x) = (x − 5)(x2 + 5x + 7), qui s'étudie plus aisément.
Exemple 2
Soit à résoudre l'équation :
6x3 − 6x2 + 12x + 7 = 0
Posons :
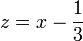
On obtient en remplaçant et en développant :
54z3 + 90z + 95 = 0
Posons alors :
z = u + v
On obtient :
54(u + v)3 + 90(u + v) + 95 = 0
Qui s'écrit :
54(u3 + v3) + (162uv + 90)(u + v) + 95 = 0
La condition de simplification sera donc :
162uv + 90 = 0
C’est-à-dire :
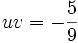
On a donc :
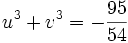
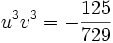
u3 et v3 sont donc les racines de l'équation :

Les deux racines de cette équation sont :

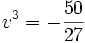
Les trois couples (u,v) vérifiant :
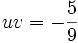
sont donc :
![u_1 = \frac{1}{3}\sqrt[3]{\frac{5}{2}}](/pictures/frwiki/57/9468485b3ff1e37f2d1d2c585eb23cdd.png) et
et ![v_1 = -\frac{1}{3}\sqrt[3]{50}](/pictures/frwiki/51/3af70922a26d4ee332f26fcb53cef876.png)
![u_2 = \frac{j}{3}\sqrt[3]{\frac{5}{2}}](/pictures/frwiki/50/25d7794f8fc7ef6f37914172cc5c5c9b.png) et
et ![v_2 = -\frac{j^2}{3}\sqrt[3]{50}](/pictures/frwiki/52/4d46d95a7c36030b97834ccad9c7cbe8.png)
![u_3 = \frac{j^2}{3}\sqrt[3]{\frac{5}{2}}](/pictures/frwiki/54/6b95a162d5edc7adb1105f00a4851382.png) et
et ![v_3 = -\frac{j}{3}\sqrt[3]{50}](/pictures/frwiki/53/503f3f3a97c92ab7a1995c004b9a046b.png)
En reportant dans :
z = u + v
On obtient :
![z_1 = \frac{1}{3}\sqrt[3]{\frac{5}{2}} - \frac{1}{3}\sqrt[3]{50}](/pictures/frwiki/97/a2233276c5a1c7fddd42a3771565513f.png)
![z_2 = \frac{j}{3}\sqrt[3]{\frac{5}{2}} - \frac{j^2}{3}\sqrt[3]{50}](/pictures/frwiki/52/4b80cbbb176b388f35992dc9384197d3.png)
![z_3 = \frac{j^2}{3}\sqrt[3]{\frac{5}{2}} - \frac{j}{3}\sqrt[3]{50}](/pictures/frwiki/99/ca3cde0a7223d6e0387ef8026627158c.png)
Et en reportant dans :

On obtient finalement les trois solutions de l'équation que l'on s'était donné de résoudre :
![x_1 = \frac13\left(\sqrt[3]{\frac52} - \sqrt[3]{50} + 1\right)](/pictures/frwiki/102/f667ebb4671b59c2dd29093de5468970.png)
![x_2 = \frac13\left(j\sqrt[3]{\frac52} - j^2\sqrt[3]{50} + 1\right)](/pictures/frwiki/55/74ced6ca9126caf61b2db3bb7ab7aae8.png)
![x_3 = \frac13\left(j^2\sqrt[3]{\frac52} - j\sqrt[3]{50} + 1\right)](/pictures/frwiki/50/2c64d6e442f8a2bc69df6832561b636f.png)
Exemple 3
Considérons l'équation :
x3 − 6x2 + 9x − 1 = 0
Par translation P(x) = P(z + 2) = z3 − 3z + 1 = Q(z).
Posons alors :
z = u + v
On obtient :
(u + v)3 − 3(u + v) + 1 = 0
Qui s'écrit :
u3 + v3 + (3uv − 3)(u + v) + 1 = 0
La condition de simplification sera donc :
3uv − 3 = 0
C’est-à-dire :
uv = 1
On a donc :
u3 + v3 = − 1
u3v3 = 1
u3 et v3 sont donc les racines de l'équation :
X2 + X + 1 = 0
Les deux racines de cette équation sont :
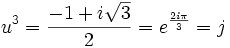
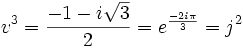
Les trois couples (u,v) vérifiant :
uv = 1
sont donc :
 et
et 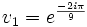
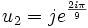 et
et 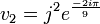
 et
et 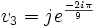
En reportant dans :
z = u + v
On obtient :
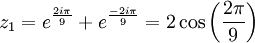
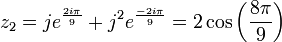
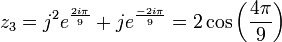
D'où les solutions en x.
Remarquons qu'en pratique, à ce niveau de mathématique, un(e) étudiant(e) se pose raisonnablement la question : ne peut-on faire mieux, au moins après-coup ? La solution fait penser à x9 − 1 = (x3 − 1)(x3 − j)(x3 − j2), et n'est-il pas possible de réagencer ce polynôme en trouvant x − 3x + 1 ? Cette notion de réagencement, de regroupement des racines devrait guider. On peut aussi penser à Q(z) = Q(iy) = iR(y).
Remarque historique
Une polémique concernant la paternité de cette méthode existe.
On raconte que la méthode fut précédemment découverte par le mathématicien italien Tartaglia. À cette époque, les mathématiciens se lançaient des défis pour résoudre des équations du troisième degré et Tartaglia les résolvait toutes. Intrigué, Cardan lui a demandé s'il n'aurait pas trouvé des méthodes. Après s'être fait prier et avoir reçu l'assurance que Cardan ne les dévoilerait à personne, Tartaglia les lui confia. Quelle ne fut pas sa surprise de voir Cardan les publier en 1545.
On appelle désormais souvent ces formules les formules de Tartaglia-Cardan.
L'utilisation des formules de Cardan nécessite parfois l'utilisation de nombres complexes, même pour trouver des solutions réelles. En fait, les nombres imaginaires sont précisément nés à cette occasion.
Dans l'exemple x3 = 15x + 4 ou bien x3 - 15x - 4 = 0, on a p = - 15 et q = -4, donc :
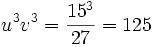 et u3 + v3 = 4 donc u3 et v3 sont racines de l'équation X2 - 4X + 125 = 0, dont les racines n'existent pas. Pourtant, il y a bien une solution x à l'équation initiale ; c'est x = 4. C'est Bombelli qui surmontera cette difficulté en proposant pour la première fois un calcul sur les nombres imaginaires. La résolution formelle de l'équation X2 - 4X + 125 = 0 donne pour racines
et u3 + v3 = 4 donc u3 et v3 sont racines de l'équation X2 - 4X + 125 = 0, dont les racines n'existent pas. Pourtant, il y a bien une solution x à l'équation initiale ; c'est x = 4. C'est Bombelli qui surmontera cette difficulté en proposant pour la première fois un calcul sur les nombres imaginaires. La résolution formelle de l'équation X2 - 4X + 125 = 0 donne pour racines  et
et  , or Bombelli s'aperçoit que le cube de
, or Bombelli s'aperçoit que le cube de 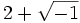 vaut
vaut 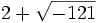 et que le cube de
et que le cube de  vaut
vaut  . Il en déduit que
. Il en déduit que 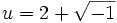 et que
et que 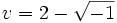 et il trouve bien comme solution finale x = u + v = 4.
et il trouve bien comme solution finale x = u + v = 4.Les nombres imaginaires sont nés.
Autres méthodes de résolution d'équations
- Méthode de Tschirnhaus
- Méthode de Bézout
- Méthode de Sotta
- Méthode de Ferrari
- Méthode de Descartes
- Méthode d'Hermite
Applet Java utilisant la méthode pour résoudre des équations du troisième degré
- Portail des mathématiques
Catégories : Nombre complexe | Équation polynomiale
Wikimedia Foundation. 2010.

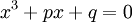
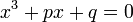
![u = \sqrt[3]{\frac{-q + \sqrt{\Delta}}{2}} \mbox{ et } v = \sqrt[3]{\frac{-q - \sqrt{\Delta}}{2}} \mbox{ soit encore } u = \sqrt[3]{-q'+\sqrt{\Delta'}} \mbox{ et } v = \sqrt[3]{-q'-\sqrt{\Delta'}}](/pictures/frwiki/101/ec7a9edda684fc46eac40488c42ce2e7.png)
![\begin{cases}x_1= 2\sqrt[3]{\frac{-q}{2}} = -2\sqrt{\frac{-p}{3}} = \frac{3q}{p} \\ x_2=x_3= -\sqrt[3]{\frac{-q}{2}} = \sqrt{\frac{-p}{3}} = \frac{-3q}{2p} \end{cases}](/pictures/frwiki/56/8b4bd1f14457317f4930b19e33b8318c.png)