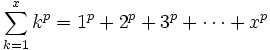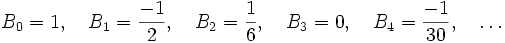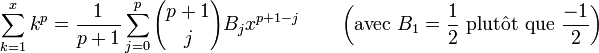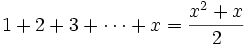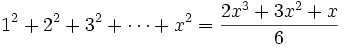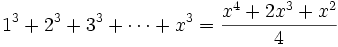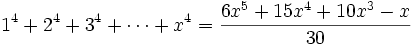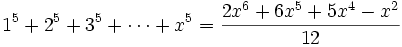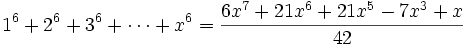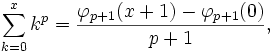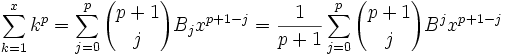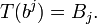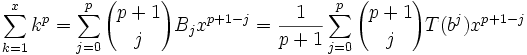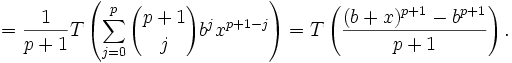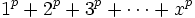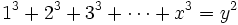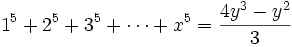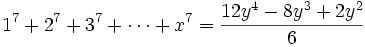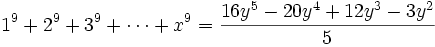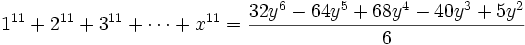Formule de faulhaber

Formule de faulhaber

Formule de Faulhaber

En mathématiques, la formule de Faulhaber, nommée en l'honneur de Johann Faulhaber, exprime la somme

\sum_{k=1}^x k^p = 1^p + 2^p + 3^p + \cdots + x^p

comme une fonction polynômiale de variable x de degré (p + 1), les coefficients impliquant les nombres de Bernoulli.

Par la convention la plus usuelle, les nombres de Bernoulli sont

B_0 = 1,\quad B_1 = {-1 \over 2},\quad B_2 = {1 \over 6}, \quad B_3 = 0,\quad B_4 = {-1 \over 30},\quad\dots

Dans l'article, nous suivront une convention vue moins souvent, 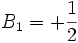B_1 = + \frac{1}{2}\,, et tous les autres nombres de Bernoulli restent comme au-dessus (voir ci-dessous pour plus de précision).

La formule s'écrit :

\sum_{k=1}^x k^p = {1 \over p+1} \sum_{j=0}^p {p+1 \choose j} B_j x^{p+1-j}\qquad \left(\mbox{avec } B_1 = {1 \over 2} \mbox{ plutôt que }{-1 \over 2}\right)

(l'index j parcours jusqu'à p, non jusqu'à p + 1).

Faulhaber ne connaissait pas la formule sous cette forme. Il connaissait au moins les 17 premiers cas et le fait que lorsque l'exposant est impair, alors la somme est une fonction polynômiale de la somme dans le cas particulier où l'exposant est 1. Il doit manipuler la factorielle n! jusqu'à 24!, ce qui illustre son remarquable talent de calculateur qu'il partage avec son correspondant Ludwig van Ceulen. Il est remarquable surtout par son anticipation des sommes multiples discrètes à une époque où l'analyse balbutie. Il utilise la k-symétrie et donne aussi certaines généralisations remarquables[1].

Sommaire

Les premiers cas

1 + 2 + 3 + \cdots + x = {x^2 + x \over 2}
1^2 + 2^2 + 3^2 + \cdots + x^2 = {2x^3 + 3x^2 + x \over 6}
1^3 + 2^3 + 3^3 + \cdots + x^3 = {x^4 + 2x^3 + x^2 \over 4}
1^4 + 2^4 + 3^4 + \cdots + x^4 = {6x^5 + 15x^4 + 10x^3 - x \over 30}
1^5 + 2^5 + 3^5 + \cdots + x^5 = {2x^6 + 6x^5 + 5x^4 - x^2 \over 12}
1^6 + 2^6 + 3^6 + \cdots + x^6 = {6x^7 + 21x^6 + 21x^5 -7x^3 + x \over 42}

Une autre forme

On peut voir la formule énoncée avec des termes parcourant de 1 à x - 1 plutôt que de 1 à x. Dans ce cas, la seule chose qui change est que nous prenons B1 = −1/2 plutôt que +1/2, donc le terme de deuxième plus haut degré dans chaque cas possède un signe moins plutôt qu'un signe plus.

Relation avec les polynômes de Bernoulli

On peut aussi écrire

\sum_{k=0}^{x} k^p = \frac{\varphi_{p+1}(x+1)-\varphi_{p+1}(0)}{p+1},

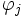où \varphi_j\, est le jème polynôme de Bernoulli.

Forme symbolique

Dans le calcul symbolique classique, on traite formellement les indices j dans une suite Bj" comme s'ils étaient des exposants, c’est-à-dire, dans ce cas nous appliquons le théorème du binôme et écrivons

\sum_{k=1}^x k^p = \sum_{j=0}^p {p+1 \choose j} B_j x^{p+1-j} = {1 \over p+1} \sum_{j=0}^p {p+1 \choose j} B^j x^{p+1-j}


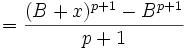= {(B+x)^{p+1} - B^{p+1} \over p+1}.

Dans le calcul symbolique « moderne », on considère la forme linéaire T sur l'espace vectoriel des polynômes de variable b donnée par

T(b^j) = B_j.\,

On peut alors écrire

\sum_{k=1}^x k^p = \sum_{j=0}^p {p+1 \choose j} B_j x^{p+1-j} = {1 \over p+1} \sum_{j=0}^p {p+1 \choose j} T(b^j) x^{p+1-j}


= {1 \over p+1} T\left(\sum_{j=0}^p {p+1 \choose j} b^j x^{p+1-j} \right) = T\left({(b+x)^{p+1} - b^{p+1} \over p+1}\right).

Polynômes de Faulhaber

La locution « polynômes de Faulhaber » est utilisée par certains auteurs pour faire référence à une autre entité que la suite de polynômes donnée ci-dessus.

Faulhaber a observé que si p est impair, alors

1^p + 2^p + 3^p + \cdots + x^p\,

est une fonction polynômiale de

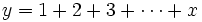y=1+2+3+\cdots+x\,.

En particulier

1^3 + 2^3 + 3^3 + \cdots + x^3 = y^2\,
1^5 + 2^5 + 3^5 + \cdots + x^5 = {4y^3 - y^2 \over 3}
1^7 + 2^7 + 3^7 + \cdots + x^7 = {12y^4 -8y^3 + 2y^2 \over 6}
1^9 + 2^9 + 3^9 + \cdots + x^9 = {16y^5 - 20y^4 +12y^3 - 3y^2 \over 5}
1^{11} + 2^{11} + 3^{11} + \cdots + x^{11} = {32y^6 - 64y^5 + 68y^4 - 40y^3 + 5y^2 \over 6}

Quelques auteurs appellent ces polynômes P(y), avec y=x(x+1)/2, « polynômes de Faulhaber ».

Bibliographie

  • John H. Conway, Richard Guy, The Book of Numbers, Spring, 1998, ISBN 038797993X, page 107
  • Eric Weisstein, CRC Concise Encyclopedia of Mathematics, Chapman & Hall/CRC, 2003, ISBN 1584883472, page 2331
  • Johann Faulhaber, « Darinnen die miraculosische Inventiones zu den höchsten Cossen weiters continuirt und profitiert werden », Academia Algebrae, Augpurg, bey Johann Ulrich Schöigs, 1631. Call number QA154.8 F3 1631a f MATH at Stanford University Libraries.

Notes et références

  1. ↑ Voir (en) texte de Knuth

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Formule de Faulhaber ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de faulhaber de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Formule De Faulhaber — En mathématiques, la formule de Faulhaber, nommée en l honneur de Johann Faulhaber, exprime la somme comme une fonction polynômiale de variable x de degré (p + 1), les coefficients impliquant les nombres de Bernoulli. Par la convention… …   Wikipédia en Français

  • Formule de Faulhaber — En mathématiques, la formule de Faulhaber, nommée en l honneur de Johann Faulhaber, exprime la somme comme une fonction polynômiale de variable x de degré (p + 1), les coefficients impliquant les nombres de Bernoulli. Par la convention… …   Wikipédia en Français

  • Formule d'Euler-Maclaurin — En mathématiques, la formule d Euler Maclaurin (appelée parfois formule sommatoire d Euler) est une relation entre sommes discrètes et intégrales. Elle fut découverte indépendamment, aux alentours de 1735, par le mathématicien suisse Leonhard… …   Wikipédia en Français

  • Johann Faulhaber — Pour les articles homonymes, voir Faulhaber. Johann Faulhaber, mathématicien allemand, né à Ulm, le 5 mai 1580, mort à Ulm, le 10 septembre 1635. Initialement tisserand, il deviendra un conseiller de la ville d Ulm. Il travaillera aux problèmes… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Nombre de Bernoulli — En mathématiques, les nombres de Bernoulli, notés (ou parfois , pour ne pas les confondre avec les polynômes de Bernoulli ou avec les nombres de Bell), constituent une suite de nombres rationnels. Les premiers nombres de Bernoulli sont donnés par …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Polynôme de Bernoulli — En mathématiques, les polynômes de Bernoulli apparaissent dans l étude de beaucoup de fonctions spéciales et en particulier, la fonction zêta de Riemann ; des polynômes analogues, correspondant à une fonction génératrice voisine, sont connus …   Wikipédia en Français

  • Preuve sans mots —  Ne doit pas être confondu avec Avec les mains. En mathématiques, une preuve sans mots (ou une démonstration visuelle) est une démonstration d une identité (ou d une affirmation mathématique plus générale) à l aide d un diagramme la rendant… …   Wikipédia en Français

  • Nombre triangulaire — Cette figure illustre le fait de 28 est le septième nombre triangulaire. En arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”