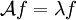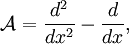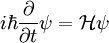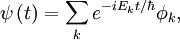Fonctions propres

Fonctions propres

Fonction propre

En mathématique

En mathématiques, une fonction propre f d'un opérateur linéaire A sur un espace de fonctions est un vecteur propre de l'opérateur linéaire. C'est une fonction non identiquement nulle et satisfaisant :

\mathcal A f = \lambda f

pour un scalaire λ, la valeur propre associée à f. L'existence de vecteurs propres est typiquement de grand secours pour analyser A.

Par exemple, pour tout réel 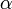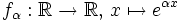\ \alpha, f_\alpha : \R \to \R,\,x \mapsto e^{\alpha x} est une fonction propre pour l'opérateur différentiel

\mathcal A = \frac{d^2}{dx^2} - \frac{d}{dx},

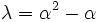avec comme valeur propre correspondante \ \lambda = \alpha^2 - \alpha.

En mécanique quantique

En mécanique quantique les fonctions propres jouent un rôle important, où l'équation de Schrödinger :

i \hbar \frac{\partial}{\partial t} \psi = \mathcal H \psi

a des solutions de la forme :

\psi\left(t\right) = \sum_k e^{-i E_k t/\hbar} \phi_k,

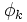où les \ \phi_k sont des fonctions propres de l'opérateur 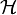\mathcal H avec les valeurs propres 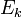\ E_k. À cause de la nature de l'opérateur hamiltonien 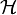\mathcal H, ces fonctions propres sont orthogonales. Cela n'est pas nécessairement le cas pour les fonctions propres d'autres opérateurs (comme l'exemple 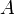\ A mentionné ci-haut).

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction propre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonctions propres de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • FONCTIONS (REPRÉSENTATION ET APPROXIMATION DES) — Il arrive très souvent que, dans les problèmes issus des mathématiques ou des autres sciences, les fonctions qui interviennent soient définies par des procédés qui ne permettent pas d’étudier de manière efficace leurs propriétés. C’est le cas des …   Encyclopédie Universelle

  • Fonctions logiques — Fonction logique Pour les articles homonymes, voir combinatoire (homonymie). Cet article se place d emblée dans le cadre de la logique classique. Il existe deux grands types de fonctions logiques : les fonctions logiques… …   Wikipédia en Français

  • Fonctions régaliennes — Régalien Régalien, ne du latin rex, regis, roi est un terme emprunté à l Histoire et qui définit ce qui est attaché à la souveraineté (peuple, roi, selon les régimes politiques). D où « fonctions régaliennes » qui regroupent les… …   Wikipédia en Français

  • Problème aux valeurs propres généralisé — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Décomposition orthogonale aux Valeurs Propres — En statistique et traitement du signal, la méthode Décomposition orthogonale aux Valeurs Propres (EOF anglicisme) consiste à décomposer des données avec des fonctions orthogonales déterminées à partir des données. C est la même chose que de faire …   Wikipédia en Français

  • Décomposition d'une matrice en éléments propres — En algèbre linéaire, la décomposition d une matrice en éléments propres est la factorisation de la factrice en une forme canonique où les coefficients matriciels sont obtenus à partir des valeurs propres et des vecteurs propres. Sommaire 1… …   Wikipédia en Français

  • Brevet d'Aptitude aux Fonctions d'Animateur en Accueils Collectifs de Mineurs — En France, le Brevet d aptitude aux fonctions d animateur en accueils collectifs de mineurs, anciennement[1] brevet d aptitude aux fonctions d animateur de centres de vacances et de loisirs, ou BAFA, est un diplôme non professionnel qui autorise… …   Wikipédia en Français

  • Brevet d'aptitude aux fonctions d'animateur — en accueils collectifs de mineurs En France, le Brevet d aptitude aux fonctions d animateur en accueils collectifs de mineurs, anciennement[1] brevet d aptitude aux fonctions d animateur de centres de vacances et de loisirs, ou BAFA, est un… …   Wikipédia en Français

  • Brevet d'aptitude aux fonctions d'animateur de centre de vacances et de loisirs — Brevet d aptitude aux fonctions d animateur en accueils collectifs de mineurs En France, le Brevet d aptitude aux fonctions d animateur en accueils collectifs de mineurs, anciennement[1] brevet d aptitude aux fonctions d animateur de centres de… …   Wikipédia en Français

  • Brevet d'aptitude aux fonctions d'animateur en accueils collectifs de mineurs — En France, le Brevet d aptitude aux fonctions d animateur en accueils collectifs de mineurs, anciennement[1] brevet d aptitude aux fonctions d animateur de centres de vacances et de loisirs, ou BAFA, est un diplôme non professionnel qui autorise… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”