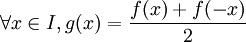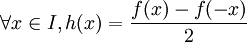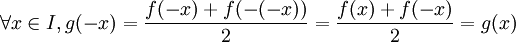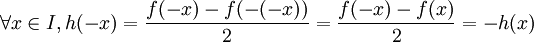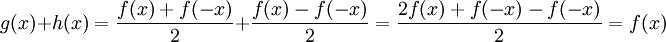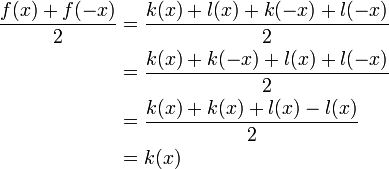Fonctions paires et impaires

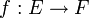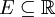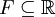En analyse, une fonction $f : E\to F$ , avec $E\subseteq\R$ et $F\subseteq\R$ est :

paire si et seulement si pour tout $x$ de $E$ , on a 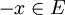$-x\in E$ et $f (x) = f ( - x)$ . Un exemple de fonction paire est la fonction cosinus ;
impaire si et seulement si pour tout $x$ de $E$ , on a 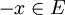$-x\in E$ et $f ( - x) = - f (x)$ . Un exemple de fonction impaire est la fonction sinus.

Les appellations « paire » et « impaire » proviennent du fait que toutes les fonctions 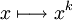$x\longmapsto x^k$ avec $k$ pair sont paires et toutes les fonctions 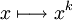$x\longmapsto x^k$ avec $k$ impair sont impaires^{[réf. souhaitée]}.

Sommaire

1 Utilisation
2 Décomposition en fonctions paires et impaires
3 Représentation graphique
4 Quelques propriétés
5 Voir aussi

Utilisation

La parité des fonctions sert par exemple à n'étudier la fonction que sur la moitié de son intervalle de définition, l'autre moitié étant déduite par symétrie. On remarquera qu'une fonction impaire centrée en 0 est nulle en ce point.

Décomposition en fonctions paires et impaires

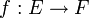Si $E$ est un sous-ensemble de $\R$ symétrique par rapport à 0 (c'est à dire que si $x$ appartient à $E$ alors $- x$ appartient à $E$ ), toute fonction $f : E\to F$ peut se décomposer comme une somme unique d'une fonction paire et d'une fonction impaire. Par conséquent, on peut parler de la partie paire de $f$ et de sa partie impaire. 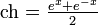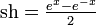Par exemple, $e x$ se décompose comme la somme unique de $\operatorname{ch} = \tfrac{e^x + e^{-x}}{2}$ et de $\operatorname{sh} = \tfrac{e^x - e^{-x}}{2}$ .

Démonstration

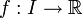Soit $I$ un sous-ensemble de $\R$ symétrique par rapport à 0 et $f : I\to\R$ .

Existence

Soient

g

h

deux fonctions de

I

dans $\R$ telles que :

$\forall x \in I, g(x) = \frac{f(x) + f(-x)}{2}$

$\forall x \in I, h(x) = \frac{f(x) - f(-x)}{2}$

On sait alors que

g

est paire car

$\forall x \in I, g(-x) = \frac{f(-x) + f(-(-x))}{2} = \frac{f(x) + f(-x)}{2} = g(x)$

et également que

h

est impaire car

$\forall x \in I, h(-x) = \frac{f(-x) - f(-(-x))}{2} = \frac{f(-x) - f(x)}{2} = -h(x)$

Ainsi

$g(x) + h(x) = \frac{f(x) + f(-x)}{2} + \frac{f(x) - f(-x)}{2} = \frac{2f(x) + f(-x) - f(-x)}{2} = f(x)$

On a donc

f = g + h

Unicité

Supposons que

f = k + l

, où 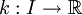$k : I\to\R$ est une fonction paire et 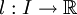$l : I\to\R$ est une fonction impaire.

$\begin{align} \frac{f(x) + f(-x)}{2} &= \frac{k(x) + l(x) + k(-x) + l(-x)}{2} \\ & = \frac{k(x) + k(-x)+ l(x) + l(-x)}{2} \\ & = \frac{k(x) + k(x)+ l(x) - l(x)}{2} \\ &= k(x) \end{align}$

On a donc que

k (x) = g (x)

et de même,

l (x) = h (x)

. La décomposition de

f = g + h

est donc unique.

Représentation graphique

Soit $f$ une fonction définie sur $E$ et $(C f)$ sa représentation graphique dans un repère orthogonal

$f$ est une fonction paire si et seulement si $(C f)$ est symétrique par rapport à l'axe $(O y)$
$f$ est une fonction impaire si et seulement si $(C f)$ est symétrique par rapport au point $O$

Mais, une fonction dont la courbe représentative possède un axe ou un centre de symétrie n'est pas forcément paire ou impaire : il est nécessaire que le centre soit $O$ ou l'axe soit $(O y)$ .

Quelques propriétés

La seule fonction qui est à la fois paire et impaire est la fonction nulle (fonction constante égale à 0).
En général, la somme d'une fonction paire et une fonction impaire n'est ni paire ni impaire ; ex : $x + x 2$ .
La somme de deux fonctions paires donne une fonction paire, et toute constante multiple d'une fonction paire est paire.
La somme de deux fonctions impaires donne une fonction impaire, et toute constante multiple d'une fonction impaire est impaire.
Le produit de deux fonctions paires donne une fonction paire.
Le produit de deux fonctions impaires donne aussi une fonction paire.
Le produit d'une fonction paire et une fonction impaire donne une fonction impaire.
Le quotient de deux fonctions paires donne une fonction paire.
Le quotient de deux fonctions impaires donne une fonction paire.
Le quotient d'une fonction paire et une fonction impaire donne une fonction impaire.
La dérivée d'une fonction paire est une fonction impaire.
La dérivée d'une fonction impaire est une fonction paire.
Une primitive d'une fonction impaire n'est pas forcément paire mais si $E$ est un intervalle, toute primitive d'une fonction impaire sur $E$ est une fonction paire.
Une primitive d'une fonction paire n'est pas forcément impaire mais si $E$ est un intervalle, la primitive d'une fonction paire sur $E$ qui s'annule en 0 est une fonction impaire.
La composée de deux fonctions impaires donne une fonction impaire.
La composée 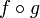$f \circ g$ d'une fonction quelconque $f$ avec une fonction paire $g$ donne une fonction paire.
La composée 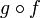$g \circ f$ d'une fonction paire $g$ avec une fonction impaire $f$ donne une fonction paire.

Voir aussi

Portail des mathématiques

Ce document provient de « Fonctions paires et impaires ».

Catégorie : Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonctions paires et impaires de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Fonctions Paires Et Impaires — En analyse, une fonction , avec et est : paire si et seulement si pour tout x de E, on a et f(x) = f( − x). Un exemple de fonction paire est la fonction cosinus&# … Wikipédia en Français
Fonctions hyperboliques — Fonction hyperbolique En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions … Wikipédia en Français
Fonction impaire — Fonctions paires et impaires En analyse, une fonction , avec et est : paire si et seulement si pour tout x de E, on a et f(x) = f( − x). Un exemple de fonction paire est la fonction cosinus&# … Wikipédia en Français
Fonction paire — Fonctions paires et impaires En analyse, une fonction , avec et est : paire si et seulement si pour tout x de E, on a et f(x) = f( − x). Un exemple de fonction paire est la fonction cosinus&# … Wikipédia en Français
Parité d'une fonction réelle — Fonctions paires et impaires En analyse, une fonction , avec et est : paire si et seulement si pour tout x de E, on a et f(x) = f( − x). Un exemple de fonction paire est la fonction cosinus&# … Wikipédia en Français
Coefficient de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Coefficients de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Décomposition d'un signal non sinusoïdal en séries de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Définition et décomposition en série de Fourier d'un signal non sinusoidal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Définition et décomposition en série de Fourier d'un signal non sinusoïdal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonctions paires et impaires