Fonction porte

Fonction porte
Page d'aide sur l'homonymie Pour les articles homonymes, voir Porte.
Graphe de la fonction porte

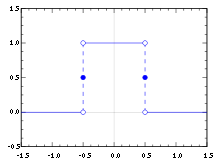
La fonction porte, généralement représentée Π, est une fonction mathématique par laquelle un nombre a une image nulle, sauf s'il est compris entre -0,5 et 0,5, auquel cas son image vaut 1. Son graphe a une forme similaire à celle d'une porte, d'où son nom.

Définition

La fonction porte est une fonction Π définie sur l'espace des réels à valeur dans {0,1} comme suit :

\forall t \in \R,\ \Pi(t) = \left \{ \begin{array}{cc} 1 & \mbox{ si } -1/2 \leq t \leq 1/2 \\ 0 & \mbox{sinon}\end{array}\right.

Par généralisation, on appelle également fonction porte toute fonction déduite par translation et/ou dilatation de la fonction définie ci-dessus. Les notations varient.

La fonction porte peut s'exprimer à l'aide de la fonction de Heaviside de cette manière :

\forall t \in \R,\ \Pi(t) = H \left(t+\frac{1}{2} \right) - H \left(t-\frac{1}{2} \right)

On peut translater la fonction porte en additionnant ou en soustrayant à t un facteur de translation (attention: la soustraction induit un retard et l'addition induit un avancement par rapport à 0). On peut élargir la porte de -1 à 1 à -a à a en divisant t par a dans l'expression de la porte originale.

Transformée de Fourier

La transformée de Fourier de la fonction porte définie ci-dessus est un sinus cardinal :

\mathcal{F}(\Pi)(f) = \mathrm{sinc}(\pi f)


Une fonction porte d'amplitude A compris entre -T/2 et T/2 s'écrit:

x(t)=0 \ si |t| > T/2
x(t)=A \ si |t| < T/2

D'après la définition de la transformée de Fourier:
X(f)=\int^{+\infty } _{-\infty} {x(t) e^{-i 2 \pi f t} \,\mathrm{d}t}
Avec i2 = − 1
Et : eix = cos(x) + isin(x)
X(f) = A\int _{-\frac{T}{2}} ^{\frac{T}{2}} \left( \cos(-2 \pi f t) + i\sin(-2 \pi f t) \right) \,\mathrm{d}t
X(f) = \frac{A}{-2 \pi f} \times \left [\sin(-2 \pi f t) \right ] ^{\frac{T}{2}} _{\frac{-T}{2}} + i\frac{A}{2 \pi f} \times \left [\cos(-2 \pi f t) \right ] ^{\frac{T}{2}} _{\frac{-T}{2}}
X(f) = \frac{-A}{2 \pi f} \times \left [ \sin \left (-2 \pi f \frac{T}{2} \right ) - \sin \left (-2 \pi f \frac{-T}{2} \right ) \right] + i \frac{A}{2 \pi f} \times \left [ \cos \left (-2 \pi f \frac{T}{2} \right ) - \cos \left (-2 \pi f \frac{-T}{2} \right ) \right]
X(f) = \frac{-2A}{2 \pi f} \times \sin \left (-2 \pi f \frac{T}{2} \right )
X(f) = {T\cdot A} \left[ \frac {\sin(-2 \pi f \frac{T}{2})}{-2 \pi f \frac{T}{2}} \right ]

X(f) = {T \cdot A} \mathrm{sinc}\left( 2 \pi f \frac{T}{2} \right )

Avec sinc, la fonction sinus cardinal.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction porte de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Fonction Porte — Pour les articles homonymes, voir Porte. Graphe de la fonction porte La fonction porte, généralement représentée Π …   Wikipédia en Français

  • Fonction De Heaviside — La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une fonction H discontinue… …   Wikipédia en Français

  • Fonction d'étape — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • Fonction d'étape de Heaviside — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • Fonction de Heavyside — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • Fonction de heaviside — La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une fonction H discontinue… …   Wikipédia en Français

  • Fonction marche de Heaviside — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • Fonction échelon — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • Fonction échelon de Heaviside — Fonction de Heaviside La fonction H0.5 de Heaviside. En mathématiques, la fonction de Heaviside (également fonction échelon, fonction marche ou, par abus de traduction de l anglais step, fonction d étape), du nom de Oliver Heaviside, est une… …   Wikipédia en Français

  • porte — 1. porte [ pɔrt ] n. f. • 1080; porta 980; lat. porta I ♦ 1 ♦ Autrefois, Ouverture spécialement aménagée dans l enceinte d une ville pour permettre le passage. « Les portes de la ville sont monumentales et surmontées de trophées dans le goût du… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”