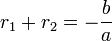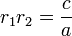- Fonction du second degre
-
Fonction du second degré
Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques En mathématiques élémentaires, une fonction du second degré est une fonction définie sur
par : 
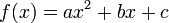où a, b et c sont des réels (a non nul) appelés les coefficients.ax2 est le terme du second degré, bx est le terme du premier degré et c est le terme constant.
Après les fonctions affines, les fonctions du second degré ou trinômes du second degré constituent le deuxième champ d'étude des fonctions polynômes.
Ces fonctions du second degré trouvent leurs applications dans des domaines extrêmement variés comme l'étude théorique d'une chute libre en physique.
Sommaire
Forme canonique
Une fonction du second degré possède une forme réduite ou forme canonique qui permet de mettre en évidence sa relation avec la fonction carré :
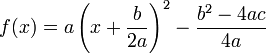
On peut remarquer que
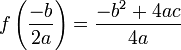
Exemple : si
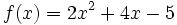, on remarque que 
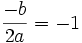et que 
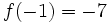donc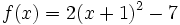 
Discriminant: On appelle discriminant le nombre Δ = b2 − 4ac. On obtient alors :
![f(x) = a\left[\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2}\right]](/pictures/frwiki/52/44b98fc89ae75ffda1520996fcc107d9.png)
De cette forme canonique se déduisent tous les résultats concernant la fonction du second degré.
Racines
Article détaillé : Équation du second degré.On dit que r est une racine de f si f(r) = 0.
On démontre que
- si Δ > 0 alors f possède deux racines qui sont
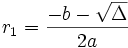et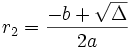 
- si Δ = 0 alors f possède une racine double qui est
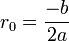
- si Δ < 0 alors f ne possède pas de racine dans l'ensemble mais il en possède dans l'ensemble
.
Cas de la racine évidente
Soit un trinôme du second degré, tel que
.
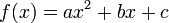Si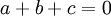
alors 
admet deux racines évidentes 
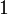et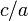 
. De même,
Si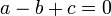
alors admet deux racines évidentes 
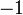et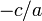 
.Opérations sur les racines
Si le polynôme du second degré possède deux racines r1 et r2 (éventuellement confondues), il est possible de connaître la sommer1 + r2 et le produit r1r2 de ces racines sans avoir besoin de les calculer au préalable.
et
Factorisation
Dans le cas où le discriminant n'est pas négatif, on peut écrire la fonction du second degré sous forme d'un produit de fonctions du premier degré.
- si
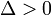alors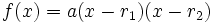 
- si
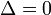alors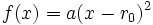 
Étude de signe
Article détaillé : Inéquation du second degré.La factorisation précédente (ou l'absence de factorisation) permet de construire le tableau de signe de
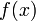. En réalité, il existe 6 cas de figure selon que 
est positif ou négatif et selon que possède 2, 1 ou 0 racines. Ces six cas de figure se résument en une méthode : «Le signe de trinôme coïncide avec celui de . sauf entre les racines»Représentation graphique
La forme canonique de la fonction
permet de remarquer que sa courbe représentative est l'image de la courbe d'équation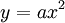 
par une translation de vecteur 
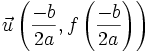.La courbe représentative est donc toujours une parabole. Son sommet est le point
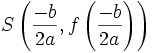et son axe de symétrie est la droite d'équation 
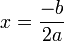.Les six paraboles ci-dessous illustrent les six cas de figures de l'étude de signe, selon le signe de
et celui de Δ. On rappelle que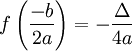 
a > 0 a < 0 Δ < 0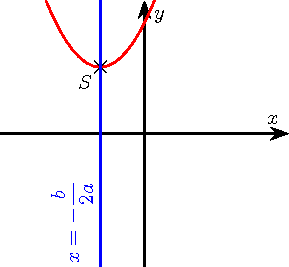 
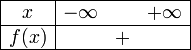
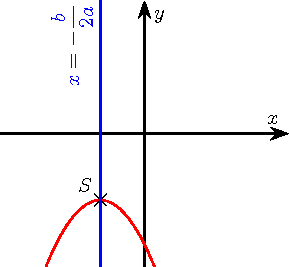
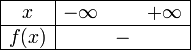
Δ = 0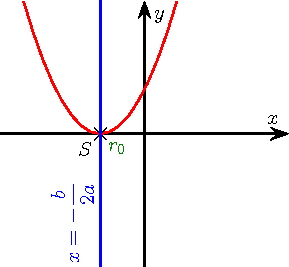 
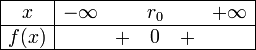
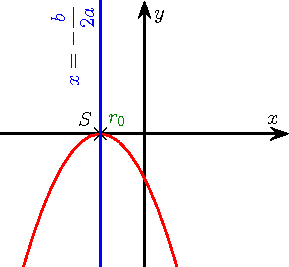
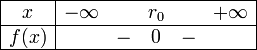
Δ > 0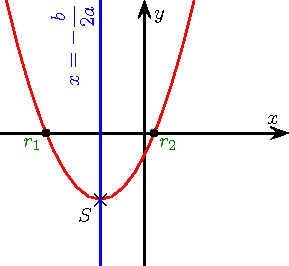 
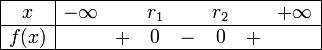
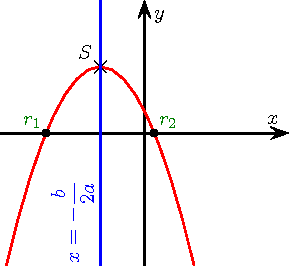
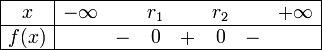
Sens de variation
Enfin, on peut déduire de cette courbe le sens de variation de
:- Si
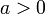, la fonction est décroissante puis croissante et atteint son minimum en 
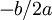; - Si
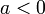, la fonction est croissante puis décroissante et atteint son maximum en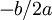
Ce résultat est confirmé par le calcul de la dérivée de
qui est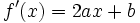 
.Liens
Portail des mathématiques
Catégorie : Mathématiques élémentaires - si Δ > 0 alors f possède deux racines qui sont
Wikimedia Foundation. 2010.
