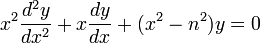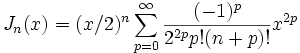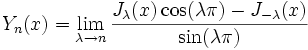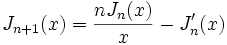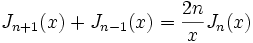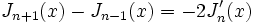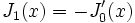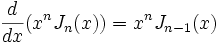Fonction de bessel

Fonction de Bessel

Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l'équation différentielle de Bessel :

$x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - n^2)y = 0$

pour tout nombre réel ou complexe n. Le cas le plus commun est quand n est un nombre naturel, et il est alors nommé l'ordre de la fonction.

Il existe deux sortes de fonctions de Bessel :

les fonctions de Bessel de première espèce J_n, solutions de l'équation différentielle ci-dessus qui sont définies en 0 ;
les fonctions de Bessel de seconde espèce Y_n, solutions qui ne sont pas définies en 0 (mais qui ont une limite infinie en 0).

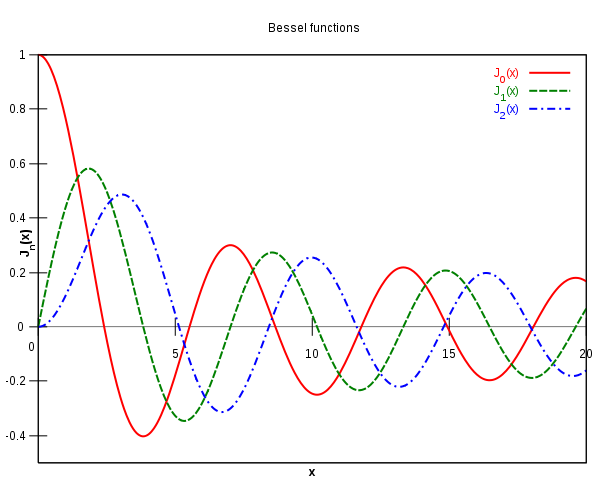
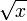Les représentations graphiques des fonctions de Bessel ressemblent à celles des fonctions sinus ou cosinus, mais s'aplanissent comme s'ils s'agissaient de fonctions sinus ou cosinus divisées par un terme de la forme $\sqrt{x}$ .

Elles sont importantes dans beaucoup de problèmes physiques.

Applications :

les ondes électromagnétiques dans un guide cylindrique (antenne) ;
les modes de vibration d'une fine membrane circulaire ou annulaire ;
l'étude d'instruments optiques ;
le pendule de Bessel ;
dans les phénomènes de diffraction par une fente circulaire.

Expression des fonctions de Bessel

Les fonctions de Bessel de première espèce Jn sont définies par :

$J_n(x)=(x/2)^n \sum_{p=0}^\infty {(-1)^p \over 2^{2p} p! (n+p)!} x^{2p}$

Les fonctions de Bessel de deuxième espèce ou fonctions de Neumann sont définies par :

$Y_n(x)=\lim_{\lambda \to n} {J_\lambda(x) \cos(\lambda \pi) - J_{-\lambda}(x) \over \sin(\lambda \pi)}$

Propriétés (des $J n$ )

Relations de récurrence :

$J_{n+1}(x)={n J_n(x) \over x}-J_n'(x)$

$J_{n+1}(x)+J_{n-1}(x)={2n \over x} J_n(x)$

$J_{n+1}(x)-J_{n-1}(x)=-2J_n'(x)\,$

On en déduit :

$J_1(x)=-J_0'(x)\;$

$\frac{d}{dx}(x^n J_n(x))=x^n J_{n-1}(x)\;$

Orthogonalité :

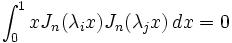
$λ i$ et $λ j$ étant deux zéros distincts de $J n$ , on a : $\int_{0}^{1} x J_n(\lambda_i x) J_n(\lambda_j x)\, dx = 0$

Liens internes

Portail des mathématiques

Ce document provient de « Fonction de Bessel ».

Catégories : Fonction remarquable | Fonction hypergéométrique | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de bessel de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Fonction De Bessel — Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n. Le cas le plus… … Wikipédia en Français
Fonction de Bessel — En mathématiques, et plus précisément en analyse, les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom du mathématicien allemand Friedrich Bessel. Bessel développa l analyse de ces fonctions en 1817… … Wikipédia en Français
fonction de Bessel — Beselio funkcija statusas T sritis fizika atitikmenys: angl. Bessel function vok. Bessel Funktion, f rus. функция Бесселя, f pranc. fonction de Bessel, f … Fizikos terminų žodynas
Fonction de Bessel modifiée — Les fonctions de Bessel modifiées génèrent l ensemble des solutions de l équation différentielle[1] . Elles sont reliées à la fonction de Bessel de première espèce Jn par[2] … Wikipédia en Français
Fonction de Bessel sphérique — Les fonctions de Bessel sphériques sont des fonctions construites à partir des fonctions de Bessel classiques et qui interviennent dans certains problèmes possédant une symétrie sphérique. Elles sont définies par : En particulier, j0… … Wikipédia en Français
BESSEL (FONCTIONS DE) — Les fonctions de Bessel jouent un rôle important en mathématiques appliquées et en physique mathématique. Elles interviennent aussi bien dans des problèmes de conduction de la chaleur que dans des problèmes de diffraction, acoustique, ou… … Encyclopédie Universelle
Bessel — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Bessel peut faire référence à : un nom de famille : Friedrich Wilhelm Bessel (1784–1846), un physicien allemand. un prénom masculin frison … Wikipédia en Français
Bessel function — Beselio funkcija statusas T sritis fizika atitikmenys: angl. Bessel function vok. Bessel Funktion, f rus. функция Бесселя, f pranc. fonction de Bessel, f … Fizikos terminų žodynas
Bessel-Funktion — Beselio funkcija statusas T sritis fizika atitikmenys: angl. Bessel function vok. Bessel Funktion, f rus. функция Бесселя, f pranc. fonction de Bessel, f … Fizikos terminų žodynas
Fonction De Hankel — Les fonctions de Hankel, du nom du mathématicien Hermann Hankel, notées et , sont des fonctions spéciales de la physique mathématique. Ce sont les solutions linéairement indépendantes de l équation de Bessel: où α est un nombre arbitraire réel ou … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de bessel