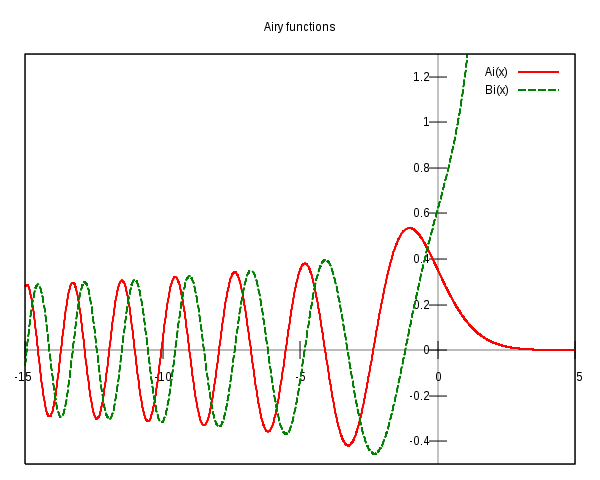
Fonction d'Airy

La fonction d'Airy Ai est une des fonctions spéciales en mathématiques, c'est-à-dire une des fonctions remarquables apparaissant fréquemment dans les calculs. Elle porte le nom de l'astronome britannique George Biddell Airy, qui l'introduisit pour ses calculs d'optique, notamment lors de l'étude de l'arc-en-ciel. La fonction d'Airy Ai et la fonction Bi, qu'on appelle fonction d'Airy de seconde espèce, sont des solutions de l'équation différentielle linéaire d'ordre deux

$y'' - xy = 0\qquad \,$

connue sous le nom d'équation d'Airy.

Sommaire

1 Définition
- 1.1 Fonction Ai
- 1.2 Fonction d'Airy de seconde espèce Bi
2 Bibliographie

Définition

La fonction Ai est en rouge et Bi en vert.

Fonction Ai

La fonction d'Airy est définie en tout x réel par la formule

$\mathrm{Ai}(x) = \frac{1}{\pi} \int_0^\infty \cos\left(\frac{t^3}{3} + xt\right)\, dt.$

qui forme une intégrale semi-convergente (cela peut être prouvé par une intégration par parties). Un théorème de dérivation des intégrales à paramètres permet de montrer que Ai est solution de l'équation d'Airy

$y'' - xy = 0\,$

avec pour conditions initiales

$\mathrm{Ai}(0) = \frac{1}{3^{2/3}\Gamma(\frac23)}, \qquad \mathrm{Ai}'(0) = -\frac{1}{3^{1/3}\Gamma(\frac13)}.$

La fonction possède notamment un point d'inflexion en x=0. Dans le domaine x>0, Ai(x) est positive, concave, et décroît exponentiellement vers 0. Dans le domaine x<0, Ai(x) oscille autour de la valeur 0 avec une fréquence de plus en plus forte et une amplitude de plus en plus faible à mesure que -x grandit. C'est ce que confirment les équivalents aux bornes (lorsque x tend vers +∞)

$\mathrm{Ai}(x) \sim \frac{e^{-\frac23x^{3/2}}}{2\sqrt\pi\,x^{1/4}} \qquad \mathrm{Ai}(-x) \sim \frac{\sin(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}}.$

dans lesquels on voit apparaître la fonction gamma.

Fonction d'Airy de seconde espèce Bi

Les solutions de l'équation d'Airy (autres que la solution nulle) ont également un comportement oscillant dans le domaine x<0. La fonction d'Airy de seconde espèce, Bi, est la solution de l'équation d'Airy dont les oscillations ont même amplitude que celles de Ai au voisinage de -∞ et qui présente un déphasage de π/2. Elle admet pour équivalents aux bornes

$\mathrm{Bi}(x) \sim \frac{e^{\frac23x^{3/2}}}{\sqrt\pi\,x^{1/4}}\qquad \mathrm{Bi}(-x) \sim \frac{\cos(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}}.$

Les fonctions Ai et Bi fonctions constituent un système fondamental de solutions de l'équation d'Airy, la seconde correspondant aux conditions initiales

$\mathrm{Bi}(0) = \frac{1}{3^{1/6}\Gamma(\frac23)}, \qquad \mathrm{Bi}'(0) = \frac{3^{1/6}}{\Gamma(\frac13)}.$

Bibliographie

G. B. Airy On the Intensity of Light in the neighbourhood of a Caustic Trans. Camb. Phil. Soc. v. 6 (1838), pp. 379-402
G. N. Watson A treatise on the theory of Bessel functions p. 188 (Cambridge, The University Press, 1922)
H. A. Antosiewicz Bessel Functions of Fractional Order in Handbook of Mathematical Functions M. Abramowitz et I. Stegun (eds.) p. 446 (US Government Printing Office, Washington DC, 1964)
O. Vallée, M. Soares Les fonctions d'Airy pour la physique (Diderot, Paris, 1998)

Portail de l'analyse

Catégories :

Fonction remarquable
Fonction spéciale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction d'Airy de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

FONCTION D’APPAREIL — Forme particulière de la fonction de transfert pour un spectromètre, la fonction d’appareil est la courbe de transmission globale obtenue en faisant défiler le spectre sur la fente de sortie, la fente d’entrée étant éclairée par une radiation… … Encyclopédie Universelle
Airy — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Airy est un nom propre qui peut désigner : Sommaire 1 Saints chrétiens 2 Personnalités … Wikipédia en Français
Fonction spéciale — Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques non élémentaires[1] … Wikipédia en Français
George Airy — George Biddell Airy Pour les articles homonymes, voir Airy. George Biddell Airy Naissance … Wikipédia en Français
George Biddell Airy — Pour les articles homonymes, voir Airy. George Biddell Airy Naissance 27 juillet 1801 Alnwick, N … Wikipédia en Français
Disque d'Airy — Tache d Airy Exemple de tache d Airy simulée par ordinateur La nature ondulatoire de la lumière fait que celle ci est diffractée après le passage à travers un trou. Plus la taille du trou diminue, plus l effet de la diffraction est visible. Le… … Wikipédia en Français
Tache d'Airy — Exemple de tache d Airy simulée par ordinateur. La nature ondulatoire de la lumière fait que celle ci est diffractée après le passage à travers un trou. Plus la taille du trou diminue, plus l effet de la diffraction est visible. Le cas… … Wikipédia en Français
Fonctions Spéciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français
Fonctions speciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français
Fonctions spéciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction d'Airy

Sommaire