F.é.m.

La force électromotrice est un des paramètres caractéristiques d'un générateur électrique. Elle est, contrairement à ce qu'indique son nom, homogène à une tension et s'exprime en volts^[1]. Dans un circuit électrique, pour mettre en mouvement des charges, il est nécessaire de fournir du travail et la force électromotrice correspond au travail que fournit un générateur au circuit par unité de charge. Pour un générateur parcouru par un courant d'intensité i et convertissant en énergie électrique, une énergie W pendant le temps t, la force électromotrice est le rapport 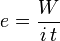. Initialement introduit par Volta pour les piles voltaïques, le concept de force électromotrice a pour base étymologique la « mise en mouvement des charges électriques ».

Pour les générateurs électrochimiques, la force électromotrice est identique à la tension à vide : lorsque l'on trace la caractéristique tension-courant d'un générateur de tension continue, la force électromotrice est l'ordonnée à l'origine du graphique. Le circuit électrique traversant le générateur lui même, une partie de ce travail est toujours dissipée à l'intérieur du générateur. L'énergie fournie au reste du circuit est inférieure à celle convertie en énergie électrique, ce qui entraîne que la tension aux bornes du générateur est inférieure à sa force électromotrice.

Suite au développement des machines électriques le terme a été étendu et la définition élargie. Ainsi pour les générateurs électromécaniques la force électromotrice, parfois nommée force électromotrice d'induction, est la circulation du champ électromoteur lié au phénomène d'induction.

Dans le cas d'un générateur, ce travail favorise effectivement la circulation des charges électriques. Il provient toujours d'un système qui converti une énergie sous une forme autre qu'électrique en énergie électrique. Dans le cas d'un récepteur, ce travail s'oppose à cette circulation. Il est transformé en une énergie autre qu'une énergie électrique. La tension qui représente cette énergie par unité de charge est alors parfois nommée force contre électromotrice.

Sommaire 1 Force électromotrice et force contre-électromotrice 2 Induction et équation de Maxwell 3 Thermodynamique 4 Notes et références 5 Articles connexes

Force électromotrice et force contre-électromotrice

La distinction entre force électromotrice d'induction et force contre-électromotrice d'induction est artificielle : le phénomène est unique.

• Si le courant, qui circule effectivement dans le conducteur, le fait selon le sens qui lui permet de s'opposer à la variation de flux alors on dit que l'on a affaire à une f.e.m. : cette f.e.m. est (parfois en partie) génératrice du courant qui circule.
• Si le courant circule dans l'autre sens, on peut la nommer force contre-électromotrice (mais ce n'est pas une obligation) car elle tend à s'opposer à la circulation du courant. Ce courant en sens inverse ne peut exister que s’il existe une autre source de tension dans le circuit qui s'oppose à la f.c.e.m. et qui délivre une valeur de tension supérieure à cette dernière.

Induction et équation de Maxwell

Lorsque le flux du champ magnétique qui traverse un circuit conducteur varie au cours du temps, il apparaît dans ce circuit une tension induite. La tension ainsi créée est orientée de façon à générer des courants s'opposant à la variation du flux. On dit donc qu'elle s'oppose à la variation du flux. La variation du flux du champ magnétique peut avoir deux causes (non exclusives) :

• Soit le circuit est soumis à un champ fixe mais on le déforme ou on l'oblige à tourner (cas des machines à courant continu).
• Soit le circuit est immobile et l'intensité du champ magnétique varie ou tourne (cas des alternateurs).

L'existence de la f.e.m. découle de l'une des équations de Maxwell, l'équation de Maxwell-Faraday :

La forme locale de cette équation est

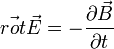
où 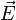est le champ électrique induit par la variation du champ magnétique .

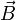Par intégration le long d'un contour conducteur C on obtient

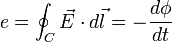
où e est la f.e.m. et ϕ est le flux magnétique traversant le circuit électrique.

Thermodynamique

La force électromotrice e étant un travail par unité de charge, le produit de la fem e par la quantité de charge dq est le travail thermodynamique reçu par les charges quant elles traversent le générateur. Ce travail peut être pris en compte dans la variation de l'énergie libre F

dF = -SdT + VdP + edq

De ce point de vue la fem et la charge sont deux variables conjuguées thermodynamiquement. Dans le cas de générateurs électrochimiques, et à pression constante, la relation précédente conduit à une relation de Maxwell qui relie la variation de tension à vide (c'est-à-dire pour une charge transférée nulle) en fonction de la température à la variation d'entropie quand la charge est transférée de façon isotherme :

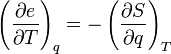
Le deuxième terme de cette relation est directement relié à l'entropie de réaction Δ_rS du processus électrochimique qui fournit au générateur son énergie.

Notes et références

Articles connexes

Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Électrostatique : Champ électrique • Charge électrique • Loi de Coulomb • Potentiel électrique
Magnétostatique : Champ magnétique • Moment magnétique • Loi de Biot et Savart
Électrocinétique : Champ électromagnétique • Courant de déplacement • Courant électrique • Ampère • Équations de Maxwell • Force électromotrice • Force de Lorentz • Induction électromagnétique • Loi de Lenz-Faraday • Rayonnement électromagnétique
Magnétisme : Diamagnétisme • Paramagnétisme • Superparamagnétisme • Ferromagnétisme • Antiferromagnétisme • Ferrimagnétisme • Loi de Curie • Domaine de Weiss • Susceptibilité magnétique • Perméabilité magnétique

• Portail de l’électricité et de l’électronique
• Portail de la physique