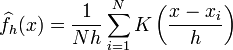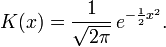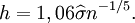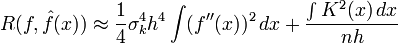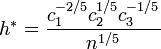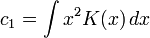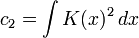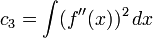Estimateur par noyau

Estimation par 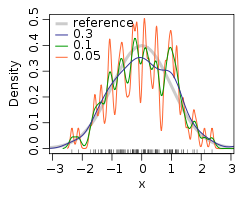la méthode du noyau d'un échantillon de 100 nombres aléatoires distribués selon la Loi normale pour différentes valeurs de la fenêtreKernel.

En statistique, l'estimation par noyau (ou encore méthode de Parzen-Rozenblatt) est une méthode non-paramétrique d'estimation de la densité de probabilité d'une variable aléatoire. Elle se base sur un échantillon d'une population statistique et permet d'estimer la densité en tout point du support. En ce sens, cette méthode généralise astucieusement la méthode d'estimation par un histogramme.

Définition

Si x₁, x₂, ..., x_N ~ ƒ est un échantillon i.i.d. d'une variable aléatoire, alors l'estimateur non-paramétrique par la méthode du noyau de la densité est

où K est un noyau (kernel en anglais) et h un paramètre nommé fenêtre, qui régit le degré de lissage de l'estimation. Bien souvent, K est choisi comme étant la densité d'une Fonction gaussienne standard (espérance nulle et variance unitaire):

Intuition

L'idée derrière la méthode de Parzen est une généralisation de la méthode d'estimation par histogramme. Dans la seconde méthode, la densité en un point x est estimée par la proportion d'observations x₁, x₂, ..., x_N qui se trouvent à proximité de x. Pour cela, on trace une boîte en x et dont la largeur est gouvernée par un paramètre de lissage h; on compte ensuite le nombre d'observations qui appartiennent à cette boîte. Cette estimation, qui dépend du paramètre de lissage h, présente de bonnes propriétés statistiques mais est par construction non-continue.

La méthode du noyau consiste à récupérer la continuité: pour cela, on remplace la boîte centrée en x et de largeur h par une courbe en cloche centrée en x. Plus une observation est proche du point de support x plus la courbe en cloche lui donnera une valeur numérique importante. A l'inverse, les observations trop éloignées de x se voient affecter une valeur numérique négligeable. L'estimateur est formé par la somme (ou plutôt la moyenne) des courbes en cloche. Comme indiqué sur l'image suivante, il est clairement continu.

Six courbes en cloche gaussiennes (rouge) et leur somme (bleu). L'estimateur à noyau de la densité f(x) est en fait la moyenne (on divise par le nombre de courbes en cloche, 6). La variance des normales est posée à 0,5. Notons enfin que plus il y a d'observations dans le voisinage d'un point, plus sa densité est élevée.

Propriétés

On peut montrer que, sous des hypothèses faibles, il n'existe pas d'estimateur non-paramétrique qui converge plus vite que l'estimateur à noyau. Notons que la vitesse de convergence n^−4/5 est plus faible que la vitesse typique des méthodes paramétriques, généralement n⁻¹.

L'utilisation pratique de cette méthode requiert deux choses:

• le noyau K (généralement la densité d'une loi statistique);
• le paramètre de lissage h.

Si le choix du noyau est réputé comme peu influent sur l'estimateur, il n'en est pas de même pour le paramètre de lissage. Un paramètre trop faible provoque l'apparition de détails artificiels apparaissant sur le graphe de l'estimateur. Pour une valeur de h trop grande, la majorité des caractéristiques est au contraire effacée. Le choix de h est donc une question centrale dans l'estimation de la densité.

Une façon répandue d'obtenir une valeur de h est de supposer que l'échantillon est distribué selon une loi paramétrique donné, par exemple selon la loi normale N(μ ; σ²). Alors, on peut prendre

Malheureusement, l'estimation gaussienne n'est pas toujours efficace, par exemple lorsque n est petit.

Une autre façon d'opérer est de chercher à fixer h de manière optimale. Soit 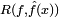la fonction de risque de l'espace L² pour ƒ. Sous des hypothèses faibles sur ƒ et K,

où

.

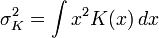La fenêtre optimale est obtenue en minimisant la fonction de risque et vaut:

où

Le paramètre h est toujours proportionnel à n ^{− 1 / 5}: c'est la constante que l'on doit rechercher. La méthode précédente n'est pas opérante dans le sens où c₃ dépend de la densité ƒ elle-même, qui est justement inconnue.

Il existe dans la littérature différentes méthodes plus sophistiquées; on se reportera avec intérêt à l'article présenté dans la bibliographie.

Implémentations en informatique

• MATLAB: la méthode est codée par la fonction ksdensity;
• R (logiciel): la méthode est codée par les scripts density et kde2d;
• SAS: il faut utiliser proc kde pour les densités univariée ou bivariée.

Bibliographie

• Parzen E. (1962). On estimation of a probability density function and mode, Ann. Math. Stat. 33, pp. 1065-1076.
• Duda, R. and Hart, P. (1973). Pattern Classification and Scene Analysis. John Wiley & Sons. ISBN 0-471-22361-1.
• Wasserman, L. (2005). All of Statistics: A Concise Course in Statistical Inference, Springer Texts in Statistics.
• B.W. Silverman. Density Estimation. London: Chapman and Hall, 1986.

Voir aussi

Articles connexes

• Noyau (statistiques)

Liens externes

• Une introduction à l'estimation par noyau;
• librairie Matlab pour l'estimation en dimension 1 et 2;
• Calculateur en ligne: calcule l'estimation par noyau avec différents noyaux possibles: Gaussien, Epanechnikov, Rectangulaire, Triangulaire, Biweight, Cosinus, et Optcosinus;
• FIGTree est une librairie efficace C++ et Matlab pour le calcul de l'estimation par noyau avec une gaussienne;
• Différentes méthodes pour sélectionner le paramètre de lissage.