Equation differentielle (mathematiques elementaires)

Equation differentielle (mathematiques elementaires)

Équation différentielle (mathématiques élémentaires)

Icone math élém.jpg
Cet article fait partie de la série
Mathématiques élémentaires
Algèbre
Logique
Arithmétique
Probabilités
Statistiques

Une équation différentielle est une équation dans laquelle la ou les inconnue(s) ne sont pas des nombres mais des fonctions et certaines de leurs dérivées. Résoudre une équation différentielle sur un intervalle I revient donc à chercher toutes les fonctions f (dérivables sur I au rang nécessaire) qui vérifient l'équation différentielle proposée.

Sommaire

Cadre général

Une équation différentielle est définie par une relation entre les fonctions inconnues recherchées et leurs dérivées à différents rangs. Par exemple l'équation:

af''+bf'+cf+d=0\,

avec des nombres réels a, b, c et d non nuls est une équation différentielle linéaire (car la relation entre f et ses dérivées est linéaire) et du second ordre (car elle contient la dérivée de f au rang 2).

Cas étudié au lycée

Définition

On s'intéresse aux équations différentielles du premier ordre, c’est-à-dire de la forme (E):af' + bf + c = 0, avec a, b et c des réels tels que a et b soient non nuls.

Les solutions dans \mathbb{R} de cette équation différentielle sont les fonctions définies par:

f(x)=ke^{-\frac{b}{a}x}-\frac{c}{b}

où k est un réel quelconque et e désigne la base du logarithme népérien. Une équation différentielle peut donc avoir une infinité de solutions car k peut prendre toutes les valeurs possibles sur \mathbb{R}.

Avec condition initiale

L'équation différentielle peut avoir une condition initiale du type f(x0) = y0 avec x0,y0 dans \mathbb{R} qui déterminera une solution particulière de l'équation différentielle.

Exemple

L'équation différentielle E définie par:

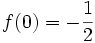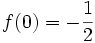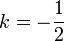2f'+f=0\, avec f(0)=-\frac{1}{2} a pour solution générale f(x)=ke^{-\frac{1}{2}x}. Comme f(0)=-\frac{1}{2}, alors -\frac{1}{2}=ke^0 d'où k=-\frac{1}{2}.

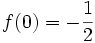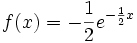On en déduit donc que la solution unique de l'équation différentielle E qui a pour condition initiale f(0)=-\frac{1}{2} est f(x)=-\frac{1}{2}e^{-\frac{1}{2}x}.


Pour approfondir, voir l'article général équation différentielle. Dans la typologie générale des équations différentielles, celles qui ont été étudiées ici sont appelées équations différentielles scalaires, linéaires, d'ordre un ou d'ordre deux, à coefficients constants.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « %C3%89quation diff%C3%A9rentielle (math%C3%A9matiques %C3%A9l%C3%A9mentaires) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equation differentielle (mathematiques elementaires) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Équation différentielle (mathématiques élémentaires) — Une équation différentielle est une équation dans laquelle la ou les inconnue(s) ne sont pas des nombres mais des fonctions et certaines de leurs dérivées. Résoudre une équation différentielle sur un intervalle I revient donc à chercher toutes… …   Wikipédia en Français

  • Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Equation différentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Équation différentielle du premier ordre — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Équation différentielle ordinaire — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Équation différentielle — En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de dérivation auquel l une des fonctions inconnues a… …   Wikipédia en Français

  • Equation (mathematiques elementaires) — Équation (mathématiques élémentaires) Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Équation (mathématiques élémentaires) — Une équation est une question, une égalité entre deux quantités algébriques. Cette égalité contient des inconnues. Résoudre l équation, c est trouver les valeurs des inconnues qui rendent vraie l égalité. En voici des exemples : 3x + 5 = 15 …   Wikipédia en Français

  • Équation différentielle stochastique — Une équation différentielle stochastique (EDS) est une généralisation de la notion d équation différentielle prenant en compte un terme de bruit blanc. Les EDS permettent de modéliser des trajectoires aléatoires, tels des cours de bourse ou les… …   Wikipédia en Français

  • Fonction exponentielle (mathématiques élémentaires) — Exponentielle Pour les articles homonymes, voir Exp. Représentation graphique de la fonction exponentielle de base e (en noir), de base 10 (en rouge) et de base 1/2 (en bleu) …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”