Afficheur 7 segments

Pour les articles homonymes, voir segment.

Un exemple de composant comportant un afficheur 7 segments

Les afficheurs 7 segments sont un type d'afficheur très présent sur les calculatrices et les montres à affichage numérique : les caractères (des chiffres, bien que quelques lettres soient utilisées pour l'affichage hexadécimal) s'écrivent en allumant ou en éteignant des segments, au nombre de sept. Quand les 7 segments sont allumés, on obtient le chiffre 8.

Caractères représentés

Animation montrant successivement les 16 caractères pouvant être représentés par un afficheur 7 segments

Voici les 10 chiffres représentés avec l'affichage à 7 segments :

• 

  0

• 

  1

• 

  2

• 

  3

• 

  4

• 

  5

• 

  6

• 

  7

• 

  8

• 

  9

Le chiffre 7 est le seul à pouvoir être représenté de deux façons : comme ici en allumant les segments A, B et C ou pour la deuxième méthode en rajoutant le segment F, cependant la deuxième méthode est assez rare.

et le complément hexadécimal :

• 

  A

• 

  B

• 

  C

• 

  D

• 

  E

• 

  F

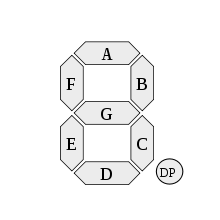
Désignation et commande des segments

Schéma montrant la désignation de chacun des segments

Dans un afficheur 7 segments, les segments sont généralement désignés par les lettres allant de A à G. Dans le cas où l'afficheur comporte un point, servant de séparateur décimal, celui-ci est désigné DP (de l'anglais decimal point) ; certains parlent dans ce cas d'un afficheur « 8 segments ».

Dans le cas d'afficheurs à DEL, deux cas de figures sont présents :

• Afficheur à anode commune : toutes les anodes sont reliées et connectées au potentiel haut.
  La commande du segment se fait par sa cathode mise au potentiel bas.
• Afficheur à cathode commune : toutes les cathodes sont reliées et connectées au potentiel bas.
  La commande du segment se fait par son anode mise au potentiel haut.

Programmation

En général, un afficheur à 7 segments se programme sur 4 bits grâce à 4 entrées conformément à la table de vérité suivante :

En notant les entrées 1, 2, 3, 4 du tableau ci-dessus respectivement i1, i2, i3 et i4, les équations des segments (pour afficher les nombres de 0 à F) sont :

• a = (not(i1) and i3) or (i1 and not(i4)) or (i2 and i3) or not(i2 or i4) or (i1 and not(i2) and not(i3)) or (not(i1) and i2 and i4)
• b = not(i1 or i2) or not(i2 or i3) or not(i2 or i4) or (not(i1) and not(i3 xor i4)) or (i1 and not(i3) and i4)
• c = (i1 xor i2) or (not(i3) and i4) or (not(i3 xor i4) and not(i2))
• d = (i1 and not(i3)) or not(i1 or i2 or i4) or (i2 and (i3 xor i4)) or (not(i2) and i3 and i4)
• e = not(i2 or i4) or (i3 and not(i4)) or (i1 and i2) or (i1 and i3)
• f = (i1 and not(i2)) or not(i3 or i4) or (not(i3) and (i1 xor i2)) or (i1 and i3) or (i2 and not(i4))
• g = (i3 and (i1 or not(i2) or not(i4))) or (i1 and i4) or (not(i3) and (i1 xor i2))

On peut retrouver ces équations en établissant la table de Karnaugh de chaque segment ; il existe d'autres possibilités de formules.

Dans le cas d'un afficheur 7 segments commandé par 8 bits, la table de vérité donne (segment G correspondant à bit 7 et A à bit 1) :

Voir aussi

• Afficheur 14 segments
• Afficheur fluorescent

• Portail de l’électricité et de l’électronique