Ensemble filtrant
- Ensemble filtrant
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Ensemble filtrant de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Ensemble Filtrant — Un ensemble filtrant est un ensemble muni d un pré ordre (relation réflexive et transitive) qui est de plus directif (un pré ordre sur un ensemble F est dit directif si quels que soient , il existe tel que et : si … Wikipédia en Français
Ensemble ordonné filtrant — Sommaire 1 Définitions 2 Exemples 3 Lien avec les filtres 4 Parties cofinales Définitions Soit … Wikipédia en Français
Limite inductive — Sommaire 1 Avant propos 2 Ensemble ordonné filtrant 3 Système inductif 4 Propriété universelle de la limite inductive … Wikipédia en Français
TOPOLOGIQUE (ALGÈBRE) — L’algèbre topologique est consacrée à l’étude d’ensembles munis d’une topologie et d’une structure algébrique définie par des lois de composition continues (cf. TOPOLOGIE, ALGÈBRE). Les exemples les plus importants sont les groupes topologiques,… … Encyclopédie Universelle
POTENTIEL ET FONCTIONS HARMONIQUES — La théorie du potentiel, directement issue de l’électrostatique, est une source d’inspiration extrêmement riche en analyse. Si, au début du XIXe siècle, on connaissait déjà l’équation de Laplace, la fonction de Green et l’intégrale de Poisson… … Encyclopédie Universelle
GÉOMÉTRIE ALGÉBRIQUE — Sous sa forme actuelle, la géométrie algébrique est une branche de l’algèbre relativement récente (cf. ALGÈBRE, DEDEKIND). Pour «comprendre» les phénomènes d’intersection des courbes et des surfaces, il s’est révélé nécessaire d’élaborer des… … Encyclopédie Universelle
coquille — [ kɔkij ] n. f. • 1262; lat. conchylium, gr. konkhulion, croisé avec lat. coccum « coque » I ♦ 1 ♦ Enveloppe calcaire qui recouvre le corps de la plupart des mollusques. ⇒ coque, coquillage, vx écaille, 1. test; exosquelette. Mollusques à… … Encyclopédie Universelle
Algebre universelle — Algèbre universelle L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de… … Wikipédia en Français
Algèbre Universelle — L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de définir de manière… … Wikipédia en Français
Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces … Wikipédia en Français
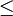 sur un ensemble F est dit directif si quels que soient
sur un ensemble F est dit directif si quels que soient 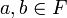 , il existe
, il existe 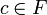 tel que
tel que 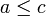 et
et 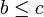 : si
: si 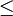 est un ordre, la propriété de directivité se résume à l'existence d'un majorant pour toute paire d'éléments de l'ensemble filtrant.)
est un ordre, la propriété de directivité se résume à l'existence d'un majorant pour toute paire d'éléments de l'ensemble filtrant.)