Ellipsoïde de révolution

Pour les articles homonymes, voir Sphéroïde.

Ellipsoïdes allongé et aplati.

En mathématiques, un ellipsoïde de révolution ou sphéroïde est une surface obtenue par rotation dans l'espace d'une ellipse autour de l'un de ses axes. Comme tout ellipsoïde, il s'agit d'une surface quadrique, c'est-à-dire qu'elle est décrite par une équation de degré 2 en chaque coordonnée dans un repère cartésien.

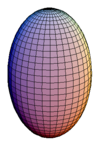
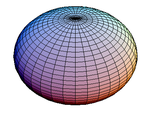
Un tel ellipsoïde peut être allongé (oblong, en anglais : prolate) si l'axe de rotation est l'axe principal (le grand axe), ce qui lui donne une forme de ballon de rugby. Dans le cas contraire, l'ellipsoïde est aplati (en anglais : oblate) comme l'approximation de la surface de la Terre.

Le mot peut aussi parfois désigner le volume borné délimité par cette surface, notamment pour décrire des objets physiques tels que la Terre ou des noyaux atomiques.

La sphère est un cas particulier d'ellipsoïde de révolution dans laquelle l'ellipse génératrice est un cercle.

Propriétés

Paramétrisation

Dans un plan de coupe contenant l'axe de rotation, la trace de l'ellipsoïde est une ellipse paramétrée en coordonnées cylindriques par un angle au centre $θ$ variant entre 0 et $2π$ sous la forme :

$\left\{\begin{array}{l} r(\theta) = q \cos(\theta) \\ z(\theta) = p \sin(\theta) \end{array}\right.$

où $p$ est le rayon polaire (longueur du demi-axe de rotation) et $q$ le rayon équatorial.

L'ellipsoïde de révolution est donc paramétré en coordonnées cartésiennes dans un repère orthonormal approprié par :

$\left\{\begin{array}{l} x(\theta, \phi) = q \cos(\theta) \cos(\phi) \\ y(\theta, \phi) = q \cos(\theta) \sin(\phi) \\ z(\theta, \phi) = p \sin(\theta) \end{array}\right.$

où l'angle de rotation $ϕ$ varie entre 0 et $π$ .

Cette paramétrisation n'est pas unique.

Équation cartésienne

La paramétrisation proposée ci-dessus fournit l'équation cartésienne :

$\frac {x^2}{q^2} + \frac {y^2}{q^2} + \frac{z^2}{p^2} = 1$

qui montre que l'ellipsoïde de révolution est une surface quadrique.

Avec ces notations, un ellipsoïde de révolution apparait comme l'image d'une sphère de rayon $q$ par une affinité de rapport $p / q$ parallèlement à l'axe de rotation.

Volume intérieur

La propriété précédente permet d'en déduire une expression du volume intérieur délimité par un ellipsoïde de révolution :

$V = \frac{4}{3}\pi p q^2$

où $p$ est le rayon polaire et $q$ le rayon à l'équateur.

Aire

L'aire d'un ellipsoïde de révolution est donné par deux formules différentes selon que l'axe de rotation de l'ellipse est son grand axe ou son petit axe. Pour lever les ambiguïtés, les notations choisies sont les notations usuelles pour les ellipses : la demi-longueur du grand axe est notée $a$ , celle du petit axe est notée $b$ , l'excentricité $e$ étant donnée par la formule^[1] :

$e = \frac{\sqrt{a^2-b^2}}{a}.$

Dans le premier cas, l'ellipsoïde est aplati, son rayon polaire étant strictement inférieur à son rayon équatorial, et l'aire est donnée par la formule :

$A = 2\pi a^2 + \frac{\pi b^2}{e} \ln\left(\frac{1+e}{1-e}\right).$

Dans le second cas, l'ellipsoïde est allongé, son rayon polaire étant strictement supérieur à son rayon équatorial, et l'aire est donnée par la formule :

$A = 2\pi b^2 + \frac{2\pi ab}{e} \mathrm{Arcsin}(e).$

Démonstration

L'aire est donnée par la formule :

$A = 2\int_0^{\pi/2}2\pi q \cos(\theta)\sqrt{q^2\sin^2(\theta)+p^2\cos^2(\theta)} \mathrm{d}\theta$

donc à l'aide du changement de variable $u = sin(θ)$ avec $d u = cos(θ)dθ$ ,

$A = 4\pi q \int_0^1\!\! \sqrt{q^2 u^2 + p^2 (1-u^2)}\ \mathrm{d}u = 4\pi q \int_0^1\!\! \sqrt{(q^2-p^2) u^2 + p^2}\ \mathrm{d}u.$

La suite des calculs dépend du signe de la différence $(q 2 - p 2)$ pour appliquer les formules des primitives de fonctions irrationnelles.

Si $q > p$: avec les égalités $q = a$ et $p = b$ , l'intégrale s'écrit :; $\int_0^1\!\! \sqrt{b^2 + (a^2-b^2)u^2}\ \mathrm{d}u = \frac{1}{2}\sqrt{a^2} + \frac{b^2}{2\sqrt{a^2-b^2}}\mathrm{argsh}\left(\frac{\sqrt{a^2-b^2}}{b}\right)$; donc l'aire se réécrit :; $A = 2\pi a^2 + \frac{2\pi b^2}{e} \mathrm{argsh}\left(\frac{\sqrt{a^2-b^2}}{b}\right).$; Or les relations entre fonctions hyperboliques réciproques permettent d'écrire :; $\mathrm{argsh}\left(\frac{\sqrt{a^2-b^2}}{b}\right) = \mathrm{argth}\left(\frac{\frac{\sqrt{a^2-b^2}}{b}}{\sqrt{\frac{a^2-b^2}{b^2}+1}}\right) = \mathrm{argth}(e) = \frac{1}{2}\ln\left(\frac{1+e}{1-e}\right).$; Donc l'aire est donnée par la formule :; $A = 2\pi a^2 + \frac{\pi b^2}{e} \ln\left(\frac{1+e}{1-e}\right).$
Si $q < p$: avec les égalités $p = a$ et $q = b$ , l'intégrale s'écrit :; $\int_0^1\!\! \sqrt{a^2 - (a^2-b^2)u^2}\ \mathrm{d}u = \frac{1}{2}\sqrt{b^2} + \frac{a^2}{2\sqrt{a^2-b^2}}\mathrm{Arcsin}\left(\frac{\sqrt{a^2-b^2}}{a}\right)$; donc l'aire se réécrit :; $A = 2\pi b^2 + \frac{2\pi ab}{e} \mathrm{Arcsin}(e).$

Applications

Plusieurs exemples d'ellipsoïdes de révolution apparaissent en physique. Par exemple, une masse fluide soumise à sa propre attraction gravitationnelle et en rotation sur elle-même forme un ellipsoïde aplati. Un autre exemple est donné par la déformation de la Terre et surtout du niveau des océans en un ellipsoïde allongé sous l'action d'un champ gravitationnel extérieur, donnant lieu au phénomène des marées.

Notes et références

↑ Cette variable $e$ n'a aucun rapport avec la constante $e$ , base du logarithme népérien.

Voir aussi

Catégorie :

Surface

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ellipsoïde de révolution de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Ellipsoide de revolution — Ellipsoïde de révolution Une ellipsoïde de révolution est un modèle géométrique couramment utilisé pour approximer une géoïde. Chaque système géodésique (repère dans lequel sont calculées les coordonnées GPS par exemple) dépend d une ellipsoïde… … Wikipédia en Français
Ellipsoïde De Révolution — Une ellipsoïde de révolution est un modèle géométrique couramment utilisé pour approximer une géoïde. Chaque système géodésique (repère dans lequel sont calculées les coordonnées GPS par exemple) dépend d une ellipsoïde de révolution. Elle permet … Wikipédia en Français
Ellipsoïde de révolution — ● Ellipsoïde de révolution ellipsoïde dont une équation est , avec a = b ≠ c. (Son volume intérieur est égal à ) … Encyclopédie Universelle
ellipsoïde de révolution — sukimosi elipsoidas statusas T sritis fizika atitikmenys: angl. ellipsoid of revolution vok. Drehellipsoid, n; Rotationsellipsoid, n rus. эллипсоид вращения, m pranc. ellipsoïde de révolution, m … Fizikos terminų žodynas
ellipsoïde — [ elipsɔid ] n. m. et adj. • 1705; de 2. ellipse et oïde ♦ Math. 1 ♦ Quadrique dont les sections planes sont des ellipses. Ellipsoïde de révolution : solide engendré par une ellipse tournant autour d un de ses axes (allongé, autour du grand axe;… … Encyclopédie Universelle
Ellipsoide — Ellipsoïde En mathématiques, un ellipsoïde est une surface du second degré de l espace euclidien à trois dimensions. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de point à l infini. Ellipsoïde avec… … Wikipédia en Français
Ellipsoide de Bessel — Ellipsoïde de Bessel L ellipsoïde de Bessel (encore appelé Bessel 1841) est un ellipsoïde de référence utilisé pour l Europe. Friedrich Wilhelm Bessel l a calculé en 1841 à partir d un important recueil de données topographiques à travers l… … Wikipédia en Français
Ellipsoïde De Bessel — L ellipsoïde de Bessel (encore appelé Bessel 1841) est un ellipsoïde de référence utilisé pour l Europe. Friedrich Wilhelm Bessel l a calculé en 1841 à partir d un important recueil de données topographiques à travers l Europe (incluant la… … Wikipédia en Français
Ellipsoïde de bessel — L ellipsoïde de Bessel (encore appelé Bessel 1841) est un ellipsoïde de référence utilisé pour l Europe. Friedrich Wilhelm Bessel l a calculé en 1841 à partir d un important recueil de données topographiques à travers l Europe (incluant la… … Wikipédia en Français
révolution — [ revɔlysjɔ̃ ] n. f. • 1267 « achèvement d un cycle; écoulement d une période de temps »; bas lat. revolutio « déroulement » I ♦ Mouvement en courbe fermée. 1 ♦ Retour périodique d un astre à un point de son orbite; par ext. Marche, mouvement d… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Ellipsoïde de révolution

Sommaire