Dégénérescence (Mathématiques)
- Dégénérescence (Mathématiques)
-
Dégénérescence (mathématiques)
En mathématiques, un cas dégénéré est un cas limite dans lequel une classe d'objet change sa nature pour appartenir à une autre classe habituellement plus simple.
Parmi de nombreux exemples, on trouve :
- Le point est un cercle dégénéré, autrement dit de rayon 0. Le cercle est lui-même une forme dégénérée d'une ellipse, autrement dit avec une excentricité égale à 0.
- La droite est une forme dégénérée d'une parabole si la parabole est située dans un plan tangent. Elle est aussi la forme dégénérée d'un rectangle, s'il a un côté de longueur 0.
- Le carré est une forme dégénérée du rectangle si celui-ci a sa longueur égale à sa largeur.
- Une hyperbole peut dégénérer en deux droites qui se croisent en un point, à travers une famille d'hyperboles ayant ces droites comme asymptotes communes.
- Un système linéaire de n équations à n inconnues à généralement une solution unique. Les cas singuliers où ce système n'a pas de solution, ou a une infinité de solutions, sont les cas où le système est dit dégénéré.
- Un ensemble contenant un seul point est un continuum dégénéré.
Article détaillé : position générale.
pour d'autres exemples.
Un autre usage du mot est utilisé pour les problèmes d'algèbre linéaire : une valeur propre dégénérée est une qui possède plus d'un vecteur propre linéairement indépendant.
Rectangle dégénéré
Pour un sous-ensemble quelconque non vide d'indices  , un rectangle dégénéré borné
, un rectangle dégénéré borné 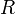 est un sous-ensemble de
est un sous-ensemble de 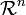 de la forme suivante :
de la forme suivante :
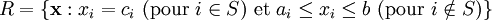
où ![\mathbf{x}= [x_1, x_2, \ldots, x_n]](/pictures/frwiki/97/adb05d00944414b0326983377d24ffa7.png) .
.
Le nombre de côtés dégénérés de 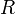 est le nombre d'éléments du sous-ensemble
est le nombre d'éléments du sous-ensemble 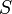 . Ainsi, il peut y avoir seulement un "côté" dégénéré ou autant que n (dans ce cas
. Ainsi, il peut y avoir seulement un "côté" dégénéré ou autant que n (dans ce cas 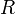 se réduit à un point unique).
se réduit à un point unique).
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Mathématiques élémentaires
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Dégénérescence (Mathématiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Degenerescence (mathematiques) — Dégénérescence (mathématiques) Pour les articles homonymes, voir Dégénérescence. En mathématiques, un cas dégénéré est un cas limite dans lequel une classe d objet change sa nature pour appartenir à une autre classe habituellement plus simple.… … Wikipédia en Français
Dégénérescence (mathématiques) — Pour les articles homonymes, voir Dégénérescence. En mathématiques, un cas dégénéré est un cas limite dans lequel une classe d objet change sa nature pour appartenir à une autre classe habituellement plus simple. Parmi de nombreux exemples, on… … Wikipédia en Français
Degenerescence — Dégénérescence Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Dégénérescence — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Dégénérescence », sur le Wiktionnaire (dictionnaire universel) En mathématiques, un cas dégénéré est… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Groupe (mathématiques) — Pour les articles homonymes, voir Groupe. Les manipulations possibles du cube de Rubik forment un groupe. En mathématiques, un groupe est un ensemble … Wikipédia en Français
Dégénérecence — Dégénérescence Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Guénon — René Guénon René Jean Marie Joseph Guénon (’Abd al Wâhid Yahyâ) Métaphysicien français naturalisé égyptien Époque moderne (XXe siècle) Photog … Wikipédia en Français
Rene Guenon — René Guénon René Jean Marie Joseph Guénon (’Abd al Wâhid Yahyâ) Métaphysicien français naturalisé égyptien Époque moderne (XXe siècle) Photog … Wikipédia en Français
 Pour les articles homonymes, voir Dégénérescence.
Pour les articles homonymes, voir Dégénérescence. , un rectangle dégénéré borné
, un rectangle dégénéré borné 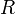 est un sous-ensemble de
est un sous-ensemble de 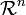 de la forme suivante :
de la forme suivante :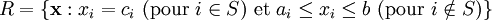
![\mathbf{x}= [x_1, x_2, \ldots, x_n]](/pictures/frwiki/97/adb05d00944414b0326983377d24ffa7.png) .
.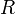 est le nombre d'éléments du sous-ensemble
est le nombre d'éléments du sous-ensemble 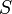 . Ainsi, il peut y avoir seulement un "côté" dégénéré ou autant que n (dans ce cas
. Ainsi, il peut y avoir seulement un "côté" dégénéré ou autant que n (dans ce cas 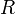 se réduit à un point unique).
se réduit à un point unique).