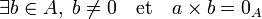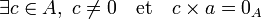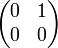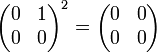Diviseurs de zéro

Diviseur de zéro

En mathématiques, un diviseur de zéro est un élément d'un anneau différent de l'élément neutre pour la première loi tel que la composition de cet élément par la deuxième loi avec un autre élément différent du neutre pour la première loi puisse donner cet élément neutre.

Définition formelle

Soient 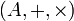$(A,+,\times)$ un anneau et 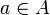$a\in A$ tel que 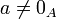$a \neq 0_A$ , où $0 A$ est l'élément neutre de la loi $+$ .

On dit que $a$ est un diviseur de zéro à gauche dans $A$ si et seulement si

$\exists b \in A,\ b \neq 0 \quad \mathrm{et} \quad a \times b=0_A$

On dit que $a$ est un diviseur de zéro à droite dans $A$ si et seulement si

$\exists c \in A,\ c \neq 0 \quad \mathrm{et} \quad c \times a=0_A$

On dit que $a$ est un diviseur de zéro dans $A$ si et seulement si $a$ est un diviseur de zéro à gauche dans $A$ et un diviseur de zéro à droite dans $A$ .

Un élément de $A$ qui n'est pas un diviseur de zéro est dit régulier.

Un diviseur de zéro ne peut pas être inversible, en particulier, un anneau admettant un diviseur de zéro ne peut pas être un corps. En effet, soit $a$ est un élément d'un anneau 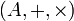$(A,+,\times)$ diviseur de zéro. On suppose que $a$ est inversible. Alors par définition il existe 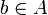$b \in A$ non nul tel que 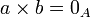$a\times b=0_A$ , et en composant par $a - 1$ à gauche il vient $b = 0 A$ , contradiction.

Anneau intègre

Article détaillé : anneau intègre.

Soit 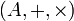$(A,+,\times)$ un anneau. Il est dit anneau intègre si et seulement s'il est non réduit à l'élément neutre et il n'admet aucun diviseur de zéro.

Exemples

Entiers relatifs et nombres réels

L'anneau 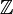$\mathbb Z$ des entiers relatifs ne contient aucun diviseur de zéro, ainsi que le corps des nombres rationnels, ou réels, ou complexes (tout corps de manière générale).

Anneau Z/nZ

Dans l'anneau 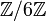$\mathbb Z/6\mathbb Z$ , la classe de 4 est un diviseur de zéro, car 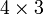$4\times 3$ est congru à 0 modulo 6, alors que 3 et 4 ne sont pas congrus à 0 modulo 6.

Plus généralement, dans l'anneau 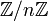$\mathbb Z/n\mathbb Z$ , les diviseurs de zéro sont exactement les classes modulo $n$ des entiers relatifs qui ne sont pas premiers avec $n$ . Cette affirmation est une simple reformulation du théorème de Bachet-Bézout.

Matrices

L’anneau 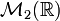$\mathcal M_2(\mathbb R)$ des matrices carrées à deux lignes et deux colonnes réelles contient des diviseurs de zéro. Par exemple, la matrice

$\begin{pmatrix}0&1\\0&0\end{pmatrix}$

est un diviseur de zéro, en effet elle est non nulle, et nous avons

$\begin{pmatrix}0&1\\0&0\end{pmatrix}^2=\begin{pmatrix}0&0\\0&0\end{pmatrix}$

Plus généralement les diviseurs de zéro à droite dans 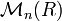$\mathcal{M}_n(R)$ sont les matrices non surjectives et les diviseurs à gauche les matrices non injectives.

Algèbre de fonctions

L'ensemble des fonctions de $\R$ dans lui-même est un anneau qui admet des diviseurs de zéro. En effet si nous prenons la fonction caractéristique des rationnels ainsi que la fonction caractéristique des irrationnels, il est clair que ces deux fonctions sont différentes de la fonction nulle, pourtant leur produit donne bien la fonction nulle, car un nombre réel est rationnel ou bien irrationnel.

Plus généralement, si $A$ est une algèbre, désignons par $A X$ l'algèbre des fonctions 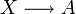$X\longrightarrow A$ , où $X$ est un ensemble non vide quelconque. Les diviseurs de zéro de $A X$ sont exactement les fonctions non nulles admettant zéro ou un diviseur de zéro dans leur image.

Portail des mathématiques

Ce document provient de « Diviseur de z%C3%A9ro ».

Catégories : Théorie des anneaux | Zéro

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Diviseurs de zéro de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Diviseur de zéro — Ne pas confondre avec la notion de division par zéro en arithmétique. En mathématiques, dans un anneau, un diviseur de zéro est un élément non nul dont le produit par un certain élément non nul est égal à zéro[1]. Sommaire … Wikipédia en Français
Diviseur De Zéro — En mathématiques, un diviseur de zéro est un élément d un anneau différent de l élément neutre pour la première loi tel que la composition de cet élément par la deuxième loi avec un autre élément différent du neutre pour la première loi puisse… … Wikipédia en Français
Diviseur de zero — Diviseur de zéro En mathématiques, un diviseur de zéro est un élément d un anneau différent de l élément neutre pour la première loi tel que la composition de cet élément par la deuxième loi avec un autre élément différent du neutre pour la… … Wikipédia en Français
Parité de zéro — Zéro objets, divisés en deux groupes égaux. Zéro est un nombre pair, étant donné qu il remplit la définition d un nombre pair : être un multiple de deux. Par conséquent, zéro partage toutes les propriétés qui découlent de cette… … Wikipédia en Français
Groupe de diviseurs — Diviseur (géométrie algébrique) Les Diviseurs de Weil et de Cartier sont des outils de la géométrie algébrique. En géométrie algébrique, comme en analyse complexe, ou en géométrie arithmétique, les diviseurs forment un groupe qui permet de saisir … Wikipédia en Français
Groupe des diviseurs — Diviseur (géométrie algébrique) Les Diviseurs de Weil et de Cartier sont des outils de la géométrie algébrique. En géométrie algébrique, comme en analyse complexe, ou en géométrie arithmétique, les diviseurs forment un groupe qui permet de saisir … Wikipédia en Français
Pseudo-anneau — Un pseudo anneau est un ensemble muni d une addition et d une multiplication qui vérifient les mêmes axiomes que celles d un anneau, à ceci près qu on n exige pas la présence d un élément neutre pour la multiplication[1]. Une minorité d auteurs… … Wikipédia en Français
ANNEAUX COMMUTATIFS — Dans tout ce qui suit, on se bornera à considérer des anneaux commutatifs unitaires, c’est à dire possédant un élément unité pour la multiplication, noté 1. Les définitions sont celles de l’article suivant, ANNEAUX ET ALGÈBRES. De nombreux cas… … Encyclopédie Universelle
Anneau commutatif — Un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. L’étude des anneaux commutatifs s’appelle l’algèbre commutative. Sommaire 1 Définition 2 Exemples 3 Histoire … Wikipédia en Français
Hypercomplexe — Nombre hypercomplexe En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Diviseurs de zéro

Diviseur de zéro

Sommaire

Définition formelle

Anneau intègre