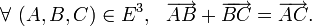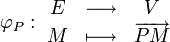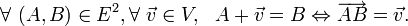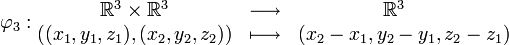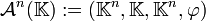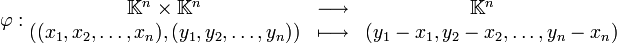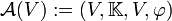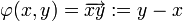- Direction d'un sous-espace affine
-
Espace affine
Historiquement, la notion d’espace affine est issue du choc dû à la découverte de nouvelles géométries parfaitement cohérentes, mais différant de celle d'Euclide par l'axiome des parallèles. Elles remettaient en cause les notions de longueur et d'angle, qui reposaient elles-mêmes sur celle de distance, et poussèrent à redéfinir l'espace euclidien, en excluant ces notions et tout ce qui s'y rapportait. Le résultat fut une géométrie affine, où l'espace apparait comme une structure algébrique, voisine de celle d'espace vectoriel qui en fut dégagée par la suite (donnant ainsi naissance à l'algèbre linéaire).
Sommaire
Définitions
Il existe de nombreuses manières de définir un espace affine (voir l'article « Structure affine »). Ici, nous supposons donnés :
- un corps (
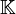 , + , x ) , noté «
, + , x ) , noté « 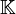 » en abrégé, d'éléments neutres « 0 » pour la loi additive et « 1 » pour la loi multiplicative ;
» en abrégé, d'éléments neutres « 0 » pour la loi additive et « 1 » pour la loi multiplicative ;
- les éléments du corps sont habituellement appelés « scalaires » et notés par des lettres grecques minuscules :
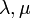 ,...
,...
- un espace vectoriel (
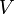 ,
, 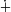 , · ) sur ce corps, noté «
, · ) sur ce corps, noté « 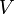 » en abrégé, d'élément neutre «
» en abrégé, d'élément neutre « 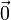 » ;
» ;
- les éléments de l'espace vectoriel sont appelés « vecteurs » et notés par des lettres latines minuscules surmontées d'une flèche :
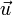 ,
, 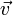 ,...
,...
- et un ensemble
 non vide, à partir duquel nous allons construire notre espace affine ;
non vide, à partir duquel nous allons construire notre espace affine ;
- ses éléments seront appelés « points » et notés par des lettres latines majuscules :
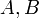 ,...
,... - remarque : les couples d'éléments de
 , éléments de
, éléments de 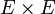 , seront appelés « bipoints », conformément à la tradition. De même, le premier élément d'un tel couple sera appelé « origine » du bipoint, et le second élément « extrémité » du bipoint.
, seront appelés « bipoints », conformément à la tradition. De même, le premier élément d'un tel couple sera appelé « origine » du bipoint, et le second élément « extrémité » du bipoint.
L'espace affine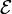 sur le corps
sur le corps 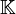 , associé à l'espace vectoriel
, associé à l'espace vectoriel 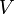 est alors défini comme le quadruplet
est alors défini comme le quadruplet 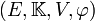 , où
, où 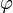 est une loi scalaire binaire, c'est-à-dire une application de
est une loi scalaire binaire, c'est-à-dire une application de 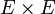 dans
dans 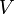 qui satisfait aux deux propriétés suivantes, appelées axiomes des espaces affines :
qui satisfait aux deux propriétés suivantes, appelées axiomes des espaces affines :- (A1) Pour tout couple de bipoints tels que l'origine du second coïncide avec l'extrémité du premier, la somme des images par
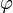 est égale à l'image, toujours par
est égale à l'image, toujours par 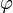 , du bipoint formé par l'origine du premier et l'extrémité du second. En d'autres termes :
, du bipoint formé par l'origine du premier et l'extrémité du second. En d'autres termes : -
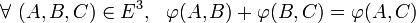
- (A2) Pour tout point et tout vecteur, il existe un unique bipoint dont l'origine est le point considéré et dont l'image par
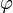 est le vecteur considéré. En d'autres termes :
est le vecteur considéré. En d'autres termes : -
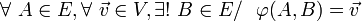
Lorsque le contexte n'est pas ambigu, la notation
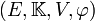 peut être abrégée, par exemple par E ou par
peut être abrégée, par exemple par E ou par 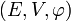 ,...
,...Si l'on note «
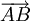 » le vecteur
» le vecteur 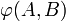 , la propriété (A1) s'écrit :
, la propriété (A1) s'écrit :Cette propriété est souvent appelée Relation de Chasles.
La propriété (A2) dit tout simplement que lorsqu'on fixe un point
 dans
dans  , l'application
, l'application 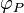 :
:est une bijection. Elle permet aussi de définir une opération (qui est plus utilisée comme une notation) correspondant à l'addition d'un vecteur à un point :
La dimension d'un espace affine est la dimension de l'espace vectoriel qui lui est associé.
L'espace vectoriel
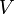 est appelé direction de
est appelé direction de 
Propriétés élémentaires
Les propriétés suivantes découlent directement de la définition d'espace affine (c'est-à-dire des axiomes (A1) et (A2)). Soient
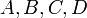 et
et 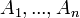 des points quelconques dans un espace affine
des points quelconques dans un espace affine 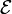 . Nous avons alors :
. Nous avons alors :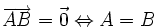 ;
;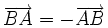 ;
;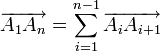 (relation de Chasles généralisée)
(relation de Chasles généralisée)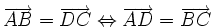 (relation du parallélogramme).
(relation du parallélogramme).
Exemples d'espaces affines
Plan affine
Regardons le plan
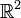 comme un ensemble de points (sans structure particulière) mais aussi comme un
comme un ensemble de points (sans structure particulière) mais aussi comme un  -espace vectoriel.
-espace vectoriel.- Le quadruplet
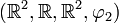 où
où 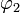 est définie par :
est définie par : -
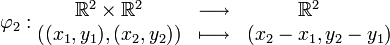
est un
 -espace affine de dimension 2 (c'est le plan affine).
-espace affine de dimension 2 (c'est le plan affine).Espace affine tridimensionnel
Le quadruplet
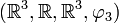 avec :
avec :est un espace affine sur
 de dimension 3.
de dimension 3.Espace affine de dimension n
De façon plus générale, si
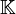 est un corps quelconque, l'espace affine canonique sur
est un corps quelconque, l'espace affine canonique sur 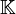 de dimension n est le quadruplet :
de dimension n est le quadruplet :où
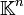 est vu à la fois comme un espace de points et un
est vu à la fois comme un espace de points et un 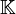 -espace vectoriel, et l'application
-espace vectoriel, et l'application  est définie par :
est définie par :Généralisation : espace affine construit à partir d'un espace vectoriel
De façon encore plus générale, si V est un espace vectoriel sur un corps
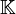 , on définit l'espace affine canonique associé à l'espace vectoriel V par le quadruplet :
, on définit l'espace affine canonique associé à l'espace vectoriel V par le quadruplet :où V est vu à la fois comme un espace de points et un
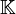 -espace vectoriel, et l'application
-espace vectoriel, et l'application  est définie par :
est définie par :Sous-espaces affines
Un sous-espace affine d'un espace affine
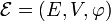 est un triplet
est un triplet 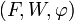 où
où  est inclus dans
est inclus dans  et
et 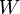 est un sous-espace vectoriel de
est un sous-espace vectoriel de 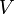 , le tout satisfaisant aux deux propriétés suivantes :
, le tout satisfaisant aux deux propriétés suivantes :- (SA1) Pour tout couple de points
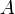 et
et 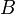 de
de  , le vecteur
, le vecteur 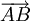 appartient à
appartient à 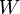 ;
;
- (SA2) Pour tout point
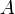 de
de  et tout vecteur
et tout vecteur 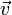 de
de 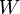 , le point
, le point 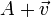 appartient à
appartient à  .
.
Le sous-espace vectoriel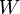 est appelé la direction du sous-espace affine. La dimension d'un sous-espace affine est tout simplement la dimension de sa direction.
est appelé la direction du sous-espace affine. La dimension d'un sous-espace affine est tout simplement la dimension de sa direction.On nomme Hyperplan affine un sous-espace affine dont la direction est un hyperplan de V.
Tout hyperplan affine peut se définir comme ensemble des points
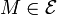 vérifiant une équation f(M) = 0, où f est une forme affine, c'est-à-dire une application affine dont la partie linéaire est une forme linéaire.
vérifiant une équation f(M) = 0, où f est une forme affine, c'est-à-dire une application affine dont la partie linéaire est une forme linéaire.Notion de parallélisme
Dans un espace affine
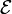 , deux sous-espaces affines
, deux sous-espaces affines 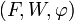 et
et 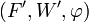 sont parallèles si l'un des sous-espaces vectoriels,
sont parallèles si l'un des sous-espaces vectoriels, 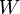 ou
ou 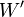 , est inclus dans l'autre.
, est inclus dans l'autre.Le célèbre cinquième postulat d'Euclide n'est alors qu'un résultat facile à démontrer à partir des définitions et des propriétés des espaces vectoriels :
Théorème (généralisation du cinquième Postulat D'Euclide) : Dans un espace affine
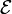 , étant donné un point quelconque
, étant donné un point quelconque  et une direction
et une direction 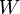 , il existe un unique sous espace affine passant par
, il existe un unique sous espace affine passant par  et ayant
et ayant 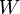 comme direction.
comme direction.A voir aussi...
- La notion d'application et de transformation affine,
- La définition de géométrie affine,
- La notion de repère affine.
- Portail des mathématiques
Catégories : Géométrie affine | Structure externe - un corps (
Wikimedia Foundation. 2010.