Diffraction par un trou circulaire

Diffraction par un trou circulaire

Tache d'Airy

Exemple de tache d'Airy simulée par ordinateur

La nature ondulatoire de la lumière fait que celle-ci est diffractée après le passage à travers un trou. Plus la taille du trou diminue, plus l'effet de la diffraction est visible.
Le cas particulier d'un trou parfaitement circulaire donne une figure de diffraction, appelée tache d'Airy (du nom de George Biddell Airy), présentant un disque central, et des cercles concentriques de plus en plus atténués. Le rayon du 1er zéro (cercle sombre) est lié à la longueur d'onde λ et à l'ouverture numérique d du dispositif :
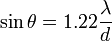
\sin \theta = 1.22 \frac{\lambda}{d}
Il ne faut pas confondre cette valeur avec la "largeur à mi-hauteur" (Full Width Half Maximum).

L'ouverture numérique caractérise le cône d'observation et est définie par le produit de la focal par par le sinus de l'angle α d'ouverture du cône en prenant en compte l'indice optique n du milieu :
d = f * n.sinα
Pour les objectifs à air, on prend n = 1 et la formule se résume à d = f.sinα, mais en microscopie optique, on utilise des milieux d'indice plus élevé (huile d'immersion, glycérol, eau) permettant d'améliorer la résolution (et aussi la luminosité).
Un effet important de cette tache, est la dégradation de la résolution des images dans les appareils optiques (appareil photographique, télescope…). Cette limite de résolution définit le critère de Rayleigh, limite de séparation entre deux objets (dépassée maintenant grâce aux techniques d'imagerie numérique et de déconvolution d'images).

Formule mathématique

L'éclairement donné par la diffraction de Fraunhofer est :

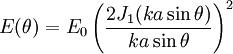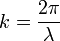E(\theta) = E_0 \left ( \frac{2 J_1(ka \sin \theta)}{ka \sin \theta} \right )^2 où J1 est la fonction de Bessel du premier ordre, et k = \frac{2 \pi}{\lambda}.


Le premier zéro de J1(x) correspond à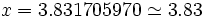 x = 3.831705970 \simeq 3.83 , donc le premier zéro de la figure de diffraction correspond à 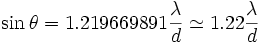\sin \theta = 1.219669891 \frac{\lambda}{d} \simeq 1.22 \frac{\lambda}{d}, où d est le diamètre du trou et a son rayon.
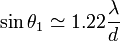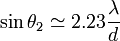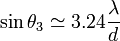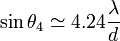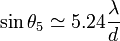Les valeurs approchées des abscisses des premiers zéros de la tache d'Airy : \sin \theta_1 \simeq 1.22\frac{\lambda}{d} ; \sin \theta_2 \simeq 2.23\frac{\lambda}{d} ; \sin \theta_3 \simeq 3.24\frac{\lambda}{d} ; \sin \theta_4 \simeq 4.24\frac{\lambda}{d} ; \sin \theta_5 \simeq 5.24\frac{\lambda}{d} .

La mi-hauteur du pic central ( J1(x) = 1/2) est atteinte pour x = 1.61633...;
Le point à 1/e² (J1(x) = 1 /e²) arrive à x = 2.58383...;
et le maximum du premier anneau est atteint pour x = 5.13562....

Voir aussi


Liens externes

Démonstration sur le site de l'Observatoire de Paris

  • Portail de la physique Portail de la physique
Ce document provient de « Tache d%27Airy ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Diffraction par un trou circulaire de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Diffraction — La diffraction est le comportement des ondes lorsqu elles rencontrent un obstacle qui ne leur est pas complètement transparent ; le phénomène peut être interprété par la diffusion d une onde par les points de l objet. La diffraction se… …   Wikipédia en Français

  • Diffraction des ondes — Diffraction La diffraction est le comportement des ondes lorsqu elles rencontrent un obstacle qui ne leur est pas complètement transparent ; le phénomène peut être interprété par la diffusion d une onde par les points de l objet. La… …   Wikipédia en Français

  • LUMIÈRE - Diffraction — On dit qu’il y a diffraction quand, dans un milieu homogène et isotrope (même vitesse de propagation pour tous les rayons lumineux quelle que soit leur direction), la lumière ne se propage pas en ligne droite. Les phénomènes de diffraction ne se… …   Encyclopédie Universelle

  • Radar Météorologique — Un radar météorologique est un type de radar utilisé en météorologie pour repérer les précipitations, calculer leur déplacement et déterminer leur type (pluie, neige, grêle, etc.). La structure tridimensionnelle des données obtenues permet… …   Wikipédia en Français

  • Radar meteorologique — Radar météorologique Un radar météorologique est un type de radar utilisé en météorologie pour repérer les précipitations, calculer leur déplacement et déterminer leur type (pluie, neige, grêle, etc.). La structure tridimensionnelle des données… …   Wikipédia en Français

  • Radar météorologique — Un radar météorologique est un type de radar utilisé en météorologie pour repérer les précipitations, calculer leur déplacement et déterminer leur type (pluie, neige, grêle, etc.). La structure tridimensionnelle des données obtenues permet… …   Wikipédia en Français

  • Radars Météorologiques — Radar météorologique Un radar météorologique est un type de radar utilisé en météorologie pour repérer les précipitations, calculer leur déplacement et déterminer leur type (pluie, neige, grêle, etc.). La structure tridimensionnelle des données… …   Wikipédia en Français

  • Radars météorologiques — Radar météorologique Un radar météorologique est un type de radar utilisé en météorologie pour repérer les précipitations, calculer leur déplacement et déterminer leur type (pluie, neige, grêle, etc.). La structure tridimensionnelle des données… …   Wikipédia en Français

  • LUNETTES ASTRONOMIQUES ET TÉLESCOPES — Sous l’appellation un peu désuète de «lunettes astronomiques» se rangent une série d’instruments d’importance historique considérable: c’est grâce, en effet, à la lunette de Galilée (fig. 1) que la conception du monde a évolué du géocentrisme… …   Encyclopédie Universelle

  • Optique géométrique — L optique géométrique est une branche de l optique qui s appuie notamment sur la notion de rayon lumineux. Cette approche simple permet notamment des constructions géométriques d images qui lui confèrent son nom. Sommaire 1 Introduction 1.1 Place …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”