Diffraction par une fente

Diffraction par une fente
Diffraction par une fente

La diffraction par une fente est un modèle théorique utilisé pour modéliser les phénomènes de diffraction en optique. La diffraction par une fente peut également s'appliquer, en raison du principe de Babinet, pour décrire la figure de diffraction obtenue avec un fil placé sur le trajet d'un rayon lumineux.

Une fente est une ouverture de largeur a et de longueur infinie, centrée sur l'origine (la fente s'étende de -a/2 à a/2 dans l'axe des x). Du fait de la symétrie par translation du problème, on ne considère les variations d'intensité que sur un seul axe x.

On se place dans le cas où l'écran est situé à l'infini (diffraction de Fraunhofer), c'est-à-dire que les rayons qui arrivent en un point M sont considérés comme parallèles. C'est le cas si l'écran est placé à plusieurs mètres de la fente, ou bien si l'on met l'écran dans le plan focal image d'une lentille convergente.

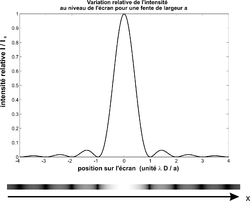
Si l'on appelle D la distance entre l'écran et la fente, alors l'intensité I en un point x de l'écran s'écrit :

I(x)= I_0 \cdot \mathrm{sinc}^2\left(\frac{\pi a}{\lambda D} \cdot x \right) ou sinc est la fonction sinus cardinal définie par sinc(x)=\frac{sin(x)}{x}

L'intensité a donc une pseudo période spatiale A valant :

A = \frac{\lambda D}{a} .

Sommaire

Formule de diffraction

Un rayon parcourt une distance δ entre la fente et l'écran. La différence de phase introduite par ce chemin est

\Delta \varphi = 2 \pi \frac{\delta}{\lambda}

λ étant la longueur d'onde de la radiation lumineuse supposée monochromatique.

Les rayons qui frappent un point de l'écran sont issus de différents points de la fente. S'ils sont en phase au niveau de la fente, leur déphasage est différent arrivé sur l'écran. Ils vont interférer, il faut donc calculer le déphasage entre les rayons pour connaître le résultat.

Considérons un point x de l'écran, et un point x1 de la fente. L'onde partant de x1 arrive en x en ayant parcouru une distance δ (d'après le théorème de Pythagore) :

\delta = \sqrt{D^2 + (x-x_1)^2} = D \cdot \sqrt{1 + \frac{(x-x_1)^2}{D^2}}

Si l'écran est suffisamment loin, on a D >> (x - x1), on peut donc faire un développement limité du premier ordre :

\delta \simeq D \cdot \left ( 1 + \frac{(x-x_1)^2}{2D^2} \right )

Si l'on développe le terme au carré :

\delta = D \cdot \left ( 1 + \frac{x^2-2xx_1 + x_1^2}{2D^2} \right )

Si l'on se place à une distance x grande devant x1 (donc devant a), on peut négliger le terme du second ordre :

\delta \simeq D \cdot \left ( 1 + \frac{x^2-2xx_1}{2D^2} \right )

Cette approximation correspond aux conditions de diffraction de Fraunhoffer.

L'onde incidente a pour fonction

\psi (t) = \psi_0 \cdot e^{i \omega t}

quel que soit x1 (onde plane, on choisit arbitrairement le déphasage nul dans le plan de la fente). Au point x, l'onde diffusée par le point x1 a pour fonction

\psi (x_1,x,t) = \psi_0 \cdot e^{i \omega t - i \Delta \varphi} = \psi_0 \cdot e^{i \omega t - i \frac{2\pi}{\lambda} D \cdot \left ( 1 + \frac{x^2-2xx_1}{2D^2} \right )}

soit

\psi (x_1,x,t) = \psi_0 \cdot e^{i \omega t - i \frac{2\pi D}{\lambda} - i \frac{\pi x^2}{\lambda D}} \cdot e^{i \frac{2\pi xx_1}{\lambda D}}

À un point x donné de l'écran, l'onde résultante vaut donc

\psi_1(x,t) = \int_{-a/2}^{a/2} \psi (x_1,x,t) dx_1 = \psi_0 \cdot e^{i \omega t - i \frac{2\pi D}{\lambda} - i \frac{\pi x^2}{\lambda D}} \cdot \int_{-a/2}^{a/2} e^{i \frac{2\pi xx_1}{\lambda D}}dx_1

Le dernier facteur vaut

- i \frac{\lambda D}{2\pi x} \cdot \left [e^{i \frac{2\pi xx_1} {\lambda D} } \right ]_{-a/2}^{a/2} = - i \frac{\lambda D}{2\pi x} \cdot \left ( e^{i \frac{\pi xa}{\lambda D}} - e^{-i \frac{\pi xa}{\lambda D}} \right ) = \frac{\lambda D}{\pi x} \cdot \sin \left ( \frac{\pi xa}{\lambda D} \right )

Donc

\psi_1(x,t) = \psi_0 \cdot e^{i \omega t - i \frac{2\pi D}{\lambda} - i \frac{\pi x^2}{\lambda D}} \cdot a \cdot \mathrm{sinc}\left ( \frac{\pi xa}{\lambda D} \right )

L'intensité lumineuse est le flux d'énergie, soit le carré de la norme

I(x) = |\psi_1(x,t)|^2 = \psi_0^2 a^2 \mathrm{sinc}^2 \left ( \frac{\pi a}{\lambda D} \cdot x \right )

Applications

La diffraction par une fente de longueur infinie permet de déterminer :

  • la figure de diffraction par une ouverture rectangulaire : c'est comme si l'on avait deux fentes infinies l'une après l'autre et tournées d'un quart de tour dans leur plan ;
  • dans le cas des deux fentes de Young, le profil dû à une fente se superpose à la figure d'interférence.

Voir aussi

Articles connexes

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Diffraction par une fente de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Diffraction Par Une Fente — La diffraction par une fente est un modèle théorique utilisé pour modéliser les phénomènes de diffraction en optique. La diffraction par une fente peut également s appliquer, en raison du principe de Babinet, pour décrire la figure de diffraction …   Wikipédia en Français

  • diffraction par une fente circulaire — difrakcija per apskritą angą statusas T sritis fizika atitikmenys: angl. diffraction by a circular aperture vok. Beugung an kreisförmiger Öffnung, f rus. дифракция на круглом отверстии, f pranc. diffraction par une fente circulaire, f;… …   Fizikos terminų žodynas

  • diffraction par une ouverture circulaire — difrakcija per apskritą angą statusas T sritis fizika atitikmenys: angl. diffraction by a circular aperture vok. Beugung an kreisförmiger Öffnung, f rus. дифракция на круглом отверстии, f pranc. diffraction par une fente circulaire, f;… …   Fizikos terminų žodynas

  • OPTIQUE CRISTALLINE - Diffraction par les cristaux — Le phénomène de diffraction de la lumière par un réseau est bien connu. Il suffit, pour s’en convaincre, de regarder la lumière d’une lampe à travers un voilage. Pour que ce phénomène soit important, il faut que la longueur d’onde du rayonnement… …   Encyclopédie Universelle

  • Diffraction — La diffraction est le comportement des ondes lorsqu elles rencontrent un obstacle qui ne leur est pas complètement transparent ; le phénomène peut être interprété par la diffusion d une onde par les points de l objet. La diffraction se… …   Wikipédia en Français

  • Diffraction des ondes — Diffraction La diffraction est le comportement des ondes lorsqu elles rencontrent un obstacle qui ne leur est pas complètement transparent ; le phénomène peut être interprété par la diffusion d une onde par les points de l objet. La… …   Wikipédia en Français

  • Diffraction De Fresnel — Fig.1 : Schéma de diffraction montrant le plan objet (contenant une ouverture ou un objet diffractant circulaire) et le plan image. En optique et électromagnétisme, la diffraction de Fresnel, encore nommée diffraction en champ proche ou… …   Wikipédia en Français

  • Diffraction de fresnel — Fig.1 : Schéma de diffraction montrant le plan objet (contenant une ouverture ou un objet diffractant circulaire) et le plan image. En optique et électromagnétisme, la diffraction de Fresnel, encore nommée diffraction en champ proche ou… …   Wikipédia en Français

  • Diffraction De Fraunhofer — Exemple de dispositif de diffraction en optique. En fonction de la position de l écran à droite, on obtient la diffraction de Fresnel (écran proche) ou celle de Fraunhofer (écran lointain) En optique et électromagnétisme, la diffraction de… …   Wikipédia en Français

  • Diffraction de fraunhofer — Exemple de dispositif de diffraction en optique. En fonction de la position de l écran à droite, on obtient la diffraction de Fresnel (écran proche) ou celle de Fraunhofer (écran lointain) En optique et électromagnétisme, la diffraction de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”