- Decomposition des ideaux premiers dans les extensions galoisiennes
-
Décomposition des idéaux premiers dans les extensions galoisiennes
En mathématiques, l'interaction entre le groupe de Galois
 d'une extension galoisienne de corps de nombres
d'une extension galoisienne de corps de nombres 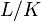 (ou de corps de nombres p-adiques, ou de corps de fonctions), et la manière dont les idéaux premiers
(ou de corps de nombres p-adiques, ou de corps de fonctions), et la manière dont les idéaux premiers  de l'anneau des entiers algébriques
de l'anneau des entiers algébriques 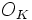 factorisent sous forme de produits d'idéaux premiers de
factorisent sous forme de produits d'idéaux premiers de 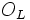 , est à la base de nombreux développement fructueux en théorie algébrique des nombres.
, est à la base de nombreux développement fructueux en théorie algébrique des nombres.Le cas d'une extension non nécessairement galoisienne est traitée dans l'article Décomposition des idéaux premiers. Les notions d'extension ramifiée, d'extension décomposée y sont envisagées ; ces notions doivent certainement être familière pour aborder la lecture du présent article. Dans le cas d'une extension galoisienne, la structure supplémentaire se traduit au niveau de ces propriétés, via, certains sous-groupes du groupe de Galois : le groupe de décomposition et le groupe d'inertie, mais aussi les groupes de ramification supérieurs.
Ces notions sont quelquefois attribuées à David Hilbert par l'appellation théorie d'Hilbert. Il existe une analogie géométrique, la ramification des surfaces de Riemann, qui est plus simple du fait qu'une seule sorte de sous-groupe de
 doit être considéré, plutôt que deux. Ceci était certainement familier avant Hilbert[réf. nécessaire].
doit être considéré, plutôt que deux. Ceci était certainement familier avant Hilbert[réf. nécessaire].Sommaire
Les propriétés fondamentales
Sur les indices
Soit la factorisation d'un idéal premier P de OK dans OL :
comme un produit d'idéaux premiers distincts
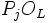 , avec les indices de ramification
, avec les indices de ramification 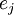 , alors
, alors  agit transitivement sur
agit transitivement sur 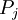 . C’est-à-dire, les facteurs idéaux premiers de P dans L forment une orbite unique sous les automorphismes de L sur K. L'unicité de la décomposition en produit d'idéaux premiers permet alors de montrer que l'indice de ramification
. C’est-à-dire, les facteurs idéaux premiers de P dans L forment une orbite unique sous les automorphismes de L sur K. L'unicité de la décomposition en produit d'idéaux premiers permet alors de montrer que l'indice de ramification 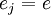 est indépendant de j. De même pour les degrés d'inertie fj, en regardant cette fois l'action du groupe de Galois sur les corps résiduels (on explique plus en détail ci-dessous cette action, ce qui est plus technique). Ces deux assertions sont fausses en général pour les extensions non galoisiennes.
est indépendant de j. De même pour les degrés d'inertie fj, en regardant cette fois l'action du groupe de Galois sur les corps résiduels (on explique plus en détail ci-dessous cette action, ce qui est plus technique). Ces deux assertions sont fausses en général pour les extensions non galoisiennes.On obtient alors la relation suivante
- [L:K] = n = efg
où g est le nombre d'idéaux premiers distincts intervenant dans la décomposition de l'idéal P.
Théorie de Galois
Cependant, la relation obtenue sur les indices ne traduit qu'une petite partie de la richesse introduite par la structure galoisienne. En effet, si g est un élément du groupe de Galois, alors g agit sur L en laissant K invariant, et, par restriction, OL en laissant OK invariant. Un idéal premier Pi de OL au-dessus d'un idéal premier P de OK étant donné, on vérifie facilement que l'action passe au quotient :
est un isomorphisme de OK/P-espaces vectoriels entre les corps résiduels. Pour obtenir un automorphisme, il est intéressant de se restreindre au cas où g(Pi)=Pi. On appelle groupe de décomposition, noté DPi de l'idéal Pi l'ensemble des éléments du groupe de Galois qui vérifient cette relation. La relation fondamentale en termes de théorie de Galois devient alors :
où le morphisme de droite est celui qu'on vient de définir. Sa surjectivité constitue un théorème. Quant à son noyau, on le définit comme étant le groupe d'inertie. Ces objets contiennent l'information qui était codé par les indices de ramification et degré d'inertie dans le cas non galoisien : le cardinal du groupe d'inertie est l'indice de ramification, celui du groupe de décomposition est le produit du degré d'inertie et de l'indice de ramification
Application de la correspondance de Galois
Les sous-corps correspondant, par la correspondance de Galois, aux sous-groupes qu'on vient de définir, admettent une interprétation arithmétique simple : le groupe de décomposition correspond à l'extension totalement décomposée maximale, et le groupe d'inertie à l'extension non ramifiée maximale.
Le symbole d'Artin
Dans le cas d'une extension non ramifiée en un premier Pi, le groupe d'inertie est trivial, comme remarqué précédemment. La relation fondamentale devient alors un isomorphisme entre le groupe de décomposition en Pi et le groupe de Galois de l'extension des corps résiduels. Dans le cas où les corps résiduels sont finis, ce qui est vrai en particulier pour les corps de nombres et les corps de nombres p-adiques, le groupe de Galois de l'extension de corps résiduels est cyclique et admet un générateur privilégié : l'endomorphisme de Frobenius. Son image dans le groupe de décomposition est alors appelé symbole d'Artin pour le premier Pi, et noté
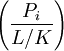 . C'est un objet à la base de la théorie des corps de classes.
. C'est un objet à la base de la théorie des corps de classes.Exemple — les entiers de Gauss
Ce paragraphe décrit la séparation des idéaux premiers dans l'extension de corps
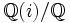 . C’est-à-dire, nous prenons
. C’est-à-dire, nous prenons 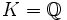 et
et 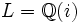 , donc
, donc 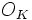 est simplement
est simplement 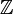 , et
, et ![O_{L} = \mathbb{Z}[i]\,](/pictures/frwiki/51/3b04ef0ebf0df0b8335d86dc300728b1.png) est l'anneau des entiers de Gauss. Bien que ce cas est loin d'être représentatif — après tout,
est l'anneau des entiers de Gauss. Bien que ce cas est loin d'être représentatif — après tout, ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) possède une décomposition en nombres premiers unique — il expose beaucoup de possibilités de la théorie.
possède une décomposition en nombres premiers unique — il expose beaucoup de possibilités de la théorie.En écrivant
 pour le groupe de Galois de
pour le groupe de Galois de 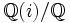 , et
, et 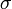 pour l'automorphisme de conjugaison complexe dans
pour l'automorphisme de conjugaison complexe dans  , il existe trois cas à considérer.
, il existe trois cas à considérer.Le nombre premier p = 2
Le nombre premier 2 de
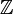 se ramifie dans
se ramifie dans ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) :
: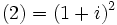 ,
,
donc ici, l'index de ramification est e = 2. Le corps de résidus est
qui est le corps avec deux éléments. Le groupe de décomposition doit être égal à tous les
 , puisqu'il existe seulement un nombre premier
, puisqu'il existe seulement un nombre premier ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) au-dessus de 2. Le groupe d'inertie est aussi tous les
au-dessus de 2. Le groupe d'inertie est aussi tous les  , puisque
, puisque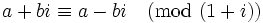 pour tout entiers a et b.
pour tout entiers a et b.
En fait, 2 est le seul nombre premier qui se ramifie dans
![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) , puisque chaque nombre premier qui se ramifie doit diviser le discriminant de
, puisque chaque nombre premier qui se ramifie doit diviser le discriminant de ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) , qui est
, qui est 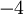 .
.Nombres premiers p ≡ 1 mod 4
Tout nombre premier
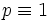 mod 4 se sépare en deux idéaux premiers distincts dans
mod 4 se sépare en deux idéaux premiers distincts dans ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) ; ceci est une manifestation du théorème de Fermat sur les sommes de deux carrés. Par exemple,
; ceci est une manifestation du théorème de Fermat sur les sommes de deux carrés. Par exemple,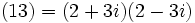 .
.
Les groupes de décomposition dans ce cas sont tous les deux le groupe trivial {1}; l'automorphisme
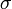 aiguille vraiment les deux nombres premiers
aiguille vraiment les deux nombres premiers 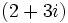 et
et 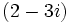 , donc il ne peut pas être dans le groupe de décomposition de chaque nombre premier. Le groupe d'inertie, étant un sous-groupe du groupe de décomposition, est aussi le groupe trivial. Il existe deux corps de résidus, un pour chaque nombre premier,
, donc il ne peut pas être dans le groupe de décomposition de chaque nombre premier. Le groupe d'inertie, étant un sous-groupe du groupe de décomposition, est aussi le groupe trivial. Il existe deux corps de résidus, un pour chaque nombre premier,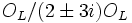 ,
,
qui sont tous les deux isomorphes au corps fini avec 13 éléments. L'élément de Frobenius est l'automorphisme trivial; ce qui signifie que
modulo
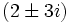 , pour tous les entiers a et b.
, pour tous les entiers a et b.Nombres premiers p ≡ 3 mod 4
Tout nombre premier
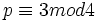 reste inerte dans
reste inerte dans ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) ; c’est-à-dire, il ne se sépare pas. Par exemple, (7) reste premier dans
; c’est-à-dire, il ne se sépare pas. Par exemple, (7) reste premier dans ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) . Dans cette situation, le groupe de décomposition sont tous les
. Dans cette situation, le groupe de décomposition sont tous les  , de nouveau parce qu'il existe seulement un seul facteur premier. Néanmoins, cette situation diffère du cas
, de nouveau parce qu'il existe seulement un seul facteur premier. Néanmoins, cette situation diffère du cas 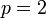 , parce que maintenant
, parce que maintenant 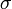 n'agit pas de manière triviale sur le corps des résidus
n'agit pas de manière triviale sur le corps des résidus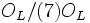 ,
,
qui est le corps fini avec
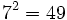 éléments. Par exemple, la différence entre
éléments. Par exemple, la différence entre 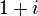 et
et  est
est 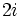 , qui est certainement non divisible par 7. Par conséquent, le groupe d'inertie est le groupe trivial {1}. Le groupe de Galois de ce corps de résidus sur le sous-corps
, qui est certainement non divisible par 7. Par conséquent, le groupe d'inertie est le groupe trivial {1}. Le groupe de Galois de ce corps de résidus sur le sous-corps 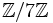 est d'ordre 2, et est engendré par l'image de l'élément de Frobenius. Le Frobenius est aucun autre que
est d'ordre 2, et est engendré par l'image de l'élément de Frobenius. Le Frobenius est aucun autre que 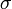 ; ce qui signifie que
; ce qui signifie quemodulo 7, pour tous les entiers a et b.
Résumé
Nombre premier dans Z Séparation dans Z[i] Groupe d'inertie Groupe de décomposition 2 se ramifie avec index 2 G G p ≡ 1 mod 4 se sépare en deux facteurs distincts 1 1 p ≡ 3 mod 4 reste inerte 1 G Un exemple
Considérons de nouveau le cas des entiers de Gauss. Nous prenons
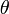 comme unité imaginaire
comme unité imaginaire 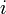 , avec le polynôme minimal
, avec le polynôme minimal 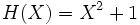 . Puisque
. Puisque ![\mathbb{Z}[i]\,](/pictures/frwiki/55/70a11c2a4372fbd5061b6923375557be.png) est l'anneau plein des entiers de
est l'anneau plein des entiers de 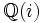 , le conducteur est l'idéal unité, donc il n'existe pas de nombres premiers exceptionnels.
, le conducteur est l'idéal unité, donc il n'existe pas de nombres premiers exceptionnels.Pour
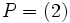 , nous devons travailler dans le corps
, nous devons travailler dans le corps 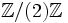 , qui contient pour factoriser le polynôme
, qui contient pour factoriser le polynôme 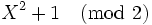 :
: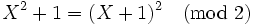 .
.
Par conséquent, il existe seulement un facteur premier, d'inertie de degré 1 et d'index de ramification 2, et ceci est donné par
Le cas suivant, P = (p) pour un nombre premier
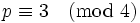 , plus concrètement, nous prendrons P = (7). Le polynôme
, plus concrètement, nous prendrons P = (7). Le polynôme 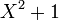 est irréductible modulo 7. Par conséquent, il existe seulement un facteur premier, d'inertie de degré 2 et d'index de ramification 1, et ceci est donné par
est irréductible modulo 7. Par conséquent, il existe seulement un facteur premier, d'inertie de degré 2 et d'index de ramification 1, et ceci est donné par![Q = (7)\mathbb{Z}[i] + (i^2 + 1)\mathbb{Z} Z[i] = 7\mathbb{Z} Z[i]](/pictures/frwiki/55/70afd1394aefe2f708a5afa7ae0e7804.png) .
.
Le dernier cas est P = (p) pour un nombre premier
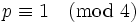 ; nous prendrons de nouveau P = (13). Cette fois, nous avons la factorisation
; nous prendrons de nouveau P = (13). Cette fois, nous avons la factorisation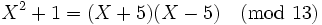 .
.
Par conséquent, il existe deux facteurs premiers, tous les deux avec un degré d'inertie et un index de ramification égal à 1. Ils sont donnés par
et
![Q_2 = (13)\mathbb{Z}[i] + (i - 5)\mathbb{Z}[i] = \cdots = (2-3i)\mathbb{Z}[i]](/pictures/frwiki/54/6977bda184da575f6e814a90dd79c618.png) .
.
Références
- (en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
- Portail des mathématiques
Catégories : Théorie algébrique des nombres | Théorie de Galois
Wikimedia Foundation. 2010.

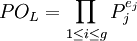
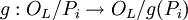
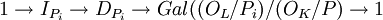
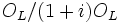
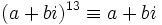
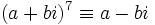
![Q = (2)\mathbb{Z}[i] + (i+1)\mathbb{Z}[i] = (1+i)\mathbb{Z}[i]\,](/pictures/frwiki/49/1ad20674bcff2b3318c6280a143765cd.png)
![Q_1 = (13)\mathbb{Z}[i] + (i + 5)\mathbb{Z}[i] = \cdots = (2+3i)\mathbb{Z}[i]](/pictures/frwiki/102/f48c91ca6c80d66949f25d0f481b66e6.png)