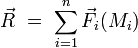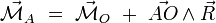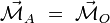- Couple (Mécanique)
-
Couple (physique)
De manière générale, en physique, on appelle couple tout système d'actions mécaniques dont la résultante
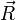 est nulle et le moment résultant
est nulle et le moment résultant 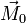 par rapport à un point O est non nul. Ce moment est alors indépendant du point O, comme démontré ci-dessous.
par rapport à un point O est non nul. Ce moment est alors indépendant du point O, comme démontré ci-dessous.En mécanique, un couple désigne l'effort en rotation appliqué à un axe. Il est ainsi nommé en raison de la façon caractéristique dont on obtient ce type d'action : un bras qui tire, un bras qui pousse, les deux forces étant égales et opposées. Lorsque le couple ne s'exerce pas rigoureusement dans l'axe, il se produit une rotation de cet axe (précession).
Sommaire
Unité de mesure
On mesure le couple en newton-mètre (N·m). L'unité de travail, le joule (J), est homogène à un newton-mètre : un couple de 1 N·m appliqué à un axe qui tourne d'un tour représente un ajout d'énergie de 2 π J. On le représente par un vecteur dans l'axe de rotation, vers le haut pour une rotation dans le sens trigonométrique (qui est l'inverse du sens des aiguilles d'une montre), comme la vitesse de rotation.
Par rapport à un mouvement rectiligne, on a les analogies suivantes :
force F (en N) couple C (en N·m) masse m (en kg) moment d'inertie I (en kg.m²) vitesse v (en m/s) vitesse angulaire w (en radian /s) énergie E = 1/2 m v² (en joules) énergie E = 1/2 I w² (en joules) puissance P = F.v (en W) puissance P = C.w (en W) accélération a = F/m (m/s²) accélération angulaire C/I (radian/s²) (attention : produit vectoriel pour la puissance)
Propriété fondamentale du couple
Rappel : moment d'une force
On rappelle que le moment par rapport à un point O d'une force dont le point d'application est au point M est défini par :
Un théorème général
Supposons le système d'actions mécaniques représentable par un ensemble dénombrable de forces
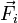 où l'indice
où l'indice 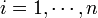 . Pour ce système d'actions mécaniques, le moment résultant est :
. Pour ce système d'actions mécaniques, le moment résultant est :Calculons alors le moment résultant par rapport à un autre point A :
On écrit que chaque vecteur position se décompose comme suit :
d'où le moment résultant :
La seconde somme représente le moment résultant en O. De plus, dans la première somme, le vecteur
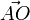 est indépendant de l'indice i ; on peut donc le sortir de la somme et écrire :
est indépendant de l'indice i ; on peut donc le sortir de la somme et écrire :La somme qui apparait n'est autre que la résultante des forces :
d'où le théorème général :
Cas particulier du couple
Le couple étant un système d'actions mécaniques dont la résultante
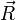 est nulle, son moment résultant est indépendant du point choisi pour le calculer :
est nulle, son moment résultant est indépendant du point choisi pour le calculer :On utilise souvent la notation
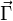 pour représenter le moment résultant d'un couple. Compte-tenu du résultat précédent, il n'est en effet pas nécessaire de préciser le point choisi pour calculer le moment.
pour représenter le moment résultant d'un couple. Compte-tenu du résultat précédent, il n'est en effet pas nécessaire de préciser le point choisi pour calculer le moment.Représentations d'un couple
Il existe une infinité de représentations différente d'un même couple
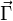 donné.
donné.Représentation la plus simple
La plus simple, qui lui donne son nom, consiste à considérer un ensemble de deux forces :
- l'une,
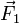 , appliqué en un point M1 différent de l'origine O fixée.
, appliqué en un point M1 différent de l'origine O fixée.
- l'autre,
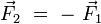 , appliqué en un point M2 symétrique du point M1 par rapport à l'origine O.
, appliqué en un point M2 symétrique du point M1 par rapport à l'origine O.
Ainsi, la résultante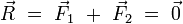 est bien nulle. On suppose de plus que les vecteurs
est bien nulle. On suppose de plus que les vecteurs 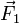 et
et 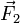 ne sont pas colinéaires au vecteur
ne sont pas colinéaires au vecteur 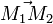 ; le cas le plus simple consiste à prendre les deux forces perpendiculaires à ce vecteur :
; le cas le plus simple consiste à prendre les deux forces perpendiculaires à ce vecteur :Si on note la distance
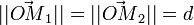 , la norme des forces
, la norme des forces 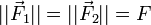 , et
, et  le vecteur unitaire perpendiculaire au plan de la figure, le couple vaut explicitement :
le vecteur unitaire perpendiculaire au plan de la figure, le couple vaut explicitement :Exemples d'autres représentations
On peut représenter le même couple
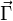 que dans l'exemple précédent par d'autres ensembles d'actions mécaniques. Par exemple, par deux forces :
que dans l'exemple précédent par d'autres ensembles d'actions mécaniques. Par exemple, par deux forces :- l'une,
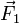 , appliqué au point O .
, appliqué au point O .
- l'autre,
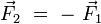 , appliqué en un point M3 situé à une distance non nulle de l'origine O.
, appliqué en un point M3 situé à une distance non nulle de l'origine O.
Ainsi, la résultante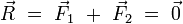 est toujours nulle. Pour simplifier, on peut encore supposer que les vecteurs
est toujours nulle. Pour simplifier, on peut encore supposer que les vecteurs 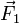 et
et 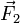 sont perpendiculaires au vecteur
sont perpendiculaires au vecteur 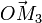 :
:
Pour retrouver la même valeur du couple :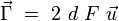 , il suffit de prendre par exemple une combinaison du type :
, il suffit de prendre par exemple une combinaison du type :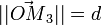 et :
et : 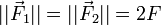
- ou :
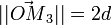 et :
et : 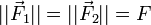
Il existe une infinité de représentations possibles ...Articles liés
Liens externes
- Portail de la physique
Catégories : Mécanique classique | Grandeur physique | Mécanique | Hydromécanique | Hydraulique
Wikimedia Foundation. 2010.

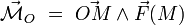
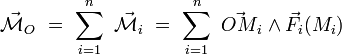
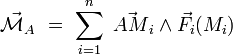
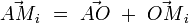
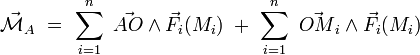
![\sum_{i=1}^n \vec{AO} \wedge \vec{F}_i(M_i) \ = \ \vec{AO} \wedge \left[ \sum_{i=1}^n \vec{F}_i(M_i) \right]](/pictures/frwiki/98/bb29e98498ae54aada6b8c696c6950f2.png)