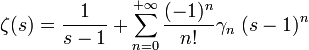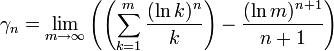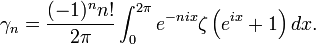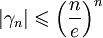Constantes de stieltjes

Constantes de Stieltjes

En mathématique, les constantes de Stieltjes (nommées d'après le mathématicien néerlandais Thomas Joannes Stieltjes) sont les nombres qui interviennent dans le développement en série de Laurent de la fonction zêta de Riemann :

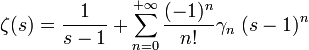
$\zeta(s) = \frac{1}{s-1} + \sum_{n=0}^{+\infty} \frac{(-1)^n}{n!} \gamma_n \; (s-1)^n$

On démontre que les $(γ n)$ sont donnés par la limite :

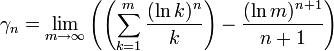
$\gamma_n = \lim_{m \rightarrow \infty} {\left( \left( \sum_{k=1}^{m} \frac{(\ln k)^n}{k} \right) - \frac{(\ln m)^{n+1}}{n+1} \right)}$

$γ 0 = γ = 0,577...$ est la constante d'Euler-Mascheroni

Voici les quelques premières valeurs :

n	Valeur
0	0,577215664901532860606512090082
1	-0,0728158454836767248605863758749
2	-0,00969036319287231848453038603521
3	0,00205383442030334586616004654275
4	0,00232537006546730005746817017753
5	0,000793323817301062701753334877444
6	-0,000238769345430199609872421841908
7	-0,000527289567057751046074097505479
8	-0,000352123353803039509602052165001
9	-0,0000343947744180880481779146237982
10	0,000205332814909064794683722289237

En utilisant la formule intégrale de Cauchy on trouve :

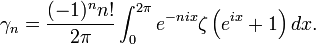
$\gamma_n = \frac{(-1)^n n!}{2\pi} \int_0^{2\pi} e^{-nix} \zeta\left(e^{ix}+1\right) dx.$

Et une comparaison série-intégrale montre que :

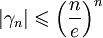
$| \gamma_n | \leqslant \left( \frac{n}{e} \right) ^ n$

Ceci dit, c'est un majorant d'une précision assez médiocre.

Voir aussi

Liens externes

Eric W. Weisstein, Constantes de Stieltjes sur MathWorld

L'inverseur de S. Plouffe. Les constantes de Stieltjes, de 0 à 78, 256 décimales de précision

Ce document provient de « Constantes de Stieltjes ».

Catégorie : Fonction zêta

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Constantes de stieltjes de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Constantes De Stieltjes — En mathématique, les constantes de Stieltjes (nommées d après le mathématicien néerlandais Thomas Joannes Stieltjes) sont les nombres qui interviennent dans le développement en série de Laurent de la fonction zêta de Riemann : On démontre… … Wikipédia en Français
Constantes de Stieltjes — En matemáticas, las constantes de Stieltjes γk son los coeficientes de la expansión en serie de Laurent de la función zeta de Riemann: Las constantes de Stieltjes se definen por el siguiente límite (En el caso n = 0, el primer sumando requiere la … Wikipedia Español
Constantes de Stieltjes — Thomas Joannes Stieltjes En mathématique, les constantes de Stieltjes (nommées d après le mathématicien néerlandais Thomas Joannes Stieltjes) sont les nombres qui interviennent dans le développement en série de Laurent de la fonction zêta de… … Wikipédia en Français
Constante de Stieltjes — Constantes de Stieltjes En mathématique, les constantes de Stieltjes (nommées d après le mathématicien néerlandais Thomas Joannes Stieltjes) sont les nombres qui interviennent dans le développement en série de Laurent de la fonction zêta de… … Wikipédia en Français
Thomas Joannes Stieltjes — Thomas Stieltjes Thomas Stieltjes Naissance 29 décembre 1856 Zwolle (Pays Bas) Décès 31 décembre 1894 … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Fonction zêta de Riemann — La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l argument de la valeur. Le point blanc pour s = 1… … Wikipédia en Français
Constante de Euler-Mascheroni — La constante de Euler Mascheroni, (también conocida como constante de Euler ) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma). Se define como el límite de la… … Wikipedia Español
Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje … Wikipedia Español
Operateur de Gauss-Kuzmin-Wirsing — Opérateur de Gauss Kuzmin Wirsing En mathématiques, l opérateur de Gauss Kuzmin Wirsing apparaît dans l étude des fractions continues. Il est aussi relié à la fonction zêta de Riemann. Sommaire 1 Introduction 2 Relation avec la fonction zêta de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Constantes de stieltjes