Connexion (mathématiques)

Connexion (mathématiques)
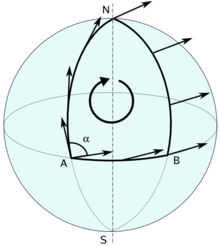
Transport parallèle sur une sphère

En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. Il existe plusieurs présentations qui dépendent de l'utilisation faite. Cette notion a été développée au début des années 1920 par Élie Cartan et Hermann Weyl (avec comme cas particulier celle de connexion affine), puis reformulée en 1951 par Charles Ehresmann et Jean-Louis Koszul.

Sommaire

Connexion de Koszul

Article détaillé : Connexion de Koszul.

La connexion de Koszul est un opérateur sur des espaces de sections. Elle a été introduite en 1951 par Koszul pour les fibrés vectoriels, et utilisée par Katsumi Nomizu en 1954[1].

Une connexion de Koszul est une association à toute section globale s d'un fibré vectoriel E de base B, et à tout champ vectoriel sur B, d'une section globale notée \nabla_Xs vérifiant :

  1. L'application X\mapsto \nabla_Xs soit C^{\infty}(M)-linéaire ; autrement dit, pour toute fonction régulière f, on a :
    \nabla_{f\cdot X}s=f\cdot\nabla_Xs.
  2. De plus, \nabla doit vérifier la relation de Leibniz :
    \nabla_{X}(f\cdot s)=df(X)\cdot s+f\cdot \nabla_X(s).

La relation de Leibniz démontre que la valeur de \nabla_Xs en un point b de B ne dépend que des variations de s au voisinage de b. La C^{\infty}(M)-linéarité implique que cette valeur ne dépend que de X(p).

Connexion de Ehresmann

Article détaillé : Connexion de Ehresmann.

Les connexions de Ehresmann sont des généralisations aux fibrés des connexions de Koszul. De façon plus précise, une connexion de Ehresmann sur E est un sous-fibré régulier H de TE, le fibré tangent de E.

Connexion de Levi-Civita

Article détaillé : Connexion de Levi-Civita.

Une métrique riemannienne g de classe Ck sur une variété différentielle M étant donnée, il existe une unique connexion de Koszul \nabla sur TxM, appelée connexion de Levi-Civita vérifiant les conditions :

  1. \nabla est sans torsion : pour tous champs de vecteurs X et Y, \nabla_XY-\nabla_YX=[X,Y] ;
  2. et g est parallèle : pour tous champs de vecteurs X, Y et Z, on a :
Z\cdot g(X,Y)=g(\nabla_ZX,Y)+g(X,\nabla_ZY).

Voir aussi

et aussi

Notes et références

Notes

  1. ↑ Katsumi Nomizu, Invariant affine connections on homogeneous spaces, Amer. J. Math. 76 (1954), p. 33-65

Références

  • (en) Marcel Berger, A Panoramic View of Riemannian Geometry [détail des éditions]
  • (en) Sylvestre Gallot, Dominique Hulin et Jacques Lafontaine, Riemannian Geometry [détail des éditions]

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Connexion (mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Connexion (Mathématiques) — Transport parallèle sur une sphère En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. La notion a été introduite par par Charles Ehresmann et Jean Louis Koszul en 1951. Il existe plusieurs présentations… …   Wikipédia en Français

  • Connexion (mathematiques) — Connexion (mathématiques) Transport parallèle sur une sphère En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. La notion a été introduite par par Charles Ehresmann et Jean Louis Koszul en 1951. Il existe …   Wikipédia en Français

  • Mathematiques de la relativite generale — Mathématiques de la relativité générale Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils… …   Wikipédia en Français

  • Mathématiques De La Relativité Générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la …   Wikipédia en Français

  • Connexion De Koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… …   Wikipédia en Français

  • Connexion de koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… …   Wikipédia en Français

  • Mathématiques de la relativité générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la …   Wikipédia en Français

  • Connexion affine — Une connexion affine sur la sphère fait rouler le plan affine tangent d un point à un autre. Dans ce déplacement, le point de contact trace une courbe du plan : le développement. En mathématiques, et plus précisément en géométrie… …   Wikipédia en Français

  • Connexion de Koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… …   Wikipédia en Français

  • Connexion — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Connexion », sur le Wiktionnaire (dictionnaire universel) D une manière générale, une connexion est l… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”