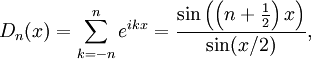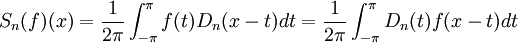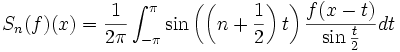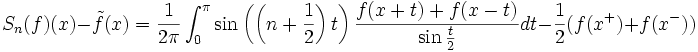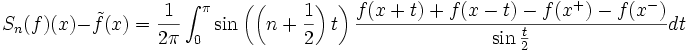Conditions de dirichlet

Conditions de dirichlet

Théorème de Dirichlet (Séries de Fourier)

En analyse, le théorème de Dirichlet (ou de Jordan-Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier.

Une première version du théorème a été prouvée par Dirichlet en 1829[1]. Faute d'une théorie de l'intégration adéquate, la preuve de Dirichlet ne permet de traiter que des fonctions assez particulières (monotones hors des points d'une subdivision).

Le théorème sera généralisé par Jordan en 1881 pour englober le cas de toutes les fonctions « localement à variations bornées »[2].

Sommaire

Énoncé

Soit ƒ une fonction définie sur \mathbb{R}, localement intégrable sur \mathbb{R} et de période 2π. Soit x0∈\mathbb{R}. On suppose que

  • ƒ admet des limites à droite et à gauche en x0, notées ƒ(x0+) et ƒ(x0-) ;
  • il existe α > 0 tel que les intégrales suivantes convergent
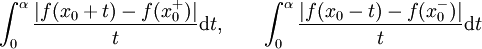\int_0^\alpha \frac{|f(x_0+t)-f(x_0^+)|}{t} {\mathrm d} t, \qquad \int_0^\alpha \frac{|f(x_0-t)-f(x_0^-)|}{t} {\mathrm d} t.

Alors, la série de Fourier de ƒ converge au point x0 et admet pour limite

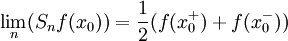\lim\limits _n (S_nf(x_0))=\frac12(f(x_0^+)+f(x_0^-)).

Notamment le théorème s'applique lorsque la fonction admet des dérivées à droite et à gauche en x0 (sans nécessairement être continue : il s'agit des dérivées à droite et à gauche des restrictions), ou encore lorsqu'elle est de classe 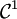\mathcal{C}^{1} par morceaux.

Démonstration

La démonstration du théorème se base sur le fait que la série de Fourier se calcule par produit de convolution avec un polynôme trigonométrique aux propriétés remarquables : le noyau de Dirichlet.

D_n(x)=\sum_{k=-n}^n e^{ikx}=\frac{\sin\left(\left(n+\frac{1}{2}\right)x\right)}{\sin(x/2)},
S_n(f)(x)=\frac1{2\pi}\int_{-\pi}^{\pi} f(t)D_n(x-t) dt=\frac1{2\pi}\int_{-\pi}^{\pi} D_n(t)f(x-t) dt

On utilise la seconde écriture du noyau de Dirichlet

S_n(f)(x)=\frac1{2\pi}\int_{-\pi}^{\pi} \sin\left(\left(n+\frac{1}{2}\right)t\right) \frac{f(x-t)}{\sin\frac t 2} dt

Cette écriture est proche de l'application du théorème de Riemann-Lebesgue, mais la fonction 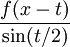\frac{f(x-t)}{\sin(t/2)} n'est pas intégrable a priori au voisinage de 0. On forme donc (en utilisant le changement de variable t'=-t pour replier la moitié de l'intégrale sur [0,π])

S_n(f)(x)-\tilde{f}(x)=\frac1{2\pi}\int_0^{\pi} \sin\left(\left(n+\frac{1}{2}\right)t\right) \frac{f(x+t)+f(x-t)}{\sin\frac t 2} dt -\frac12(f(x^+)+f(x^-))

Puis en utilisant la valeur moyenne du noyau de Dirichlet Dn on rentre les constantes dans l'intégrale :

S_n(f)(x)-\tilde{f}(x)=\frac1{2\pi}\int_0^{\pi} \sin\left(\left(n+\frac{1}{2}\right)t\right) \frac{f(x+t)+f(x-t)-f(x^+)-f(x^-)}{\sin\frac t 2} dt

Cette fois le théorème s'applique. Donc l'expression a bien une limite nulle.

Notes et références

  1. ↑ Gustav Lejeune-Dirichlet, Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, Journal de Crelle 4 (1829) p. 157-169 http://arxiv.org/abs/0806.1294
  2. ↑ Camille Jordan, Sur la série de Fourier, C. R. Acad. Sci. Paris, 92 p 228-230

Voir aussi

Bibliographie

  • Jean-Pierre Kahane, Pierre-Gilles Lemarié-Rieusset, Séries de Fourier et ondelettes [détail des éditions]

Articles connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Dirichlet (S%C3%A9ries de Fourier) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conditions de dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Conditions De Dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] …   Wikipédia en Français

  • Conditions de Dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] …   Wikipédia en Français

  • Conditions Aux Limites De Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… …   Wikipédia en Français

  • Conditions aux limites de Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… …   Wikipédia en Français

  • Conditions aux limites de dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… …   Wikipédia en Français

  • Conditions Aux Limites De Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… …   Wikipédia en Français

  • Conditions aux limites de Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… …   Wikipédia en Français

  • Conditions aux limites de neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… …   Wikipédia en Français

  • Dirichlet's theorem — may refer to any of several mathematical theorems due to Johann Peter Gustav Lejeune Dirichlet. Dirichlet s theorem on arithmetic progressions Dirichlet s approximation theorem Dirichlet s unit theorem Dirichlet conditions Dirichlet boundary… …   Wikipedia

  • Dirichlet conditions — Not to be confused with Dirichlet boundary condition. In mathematics, the Dirichlet conditions are sufficient conditions for a real valued, periodic function f(x) to be equal to the sum of its Fourier series at each point where f is continuous.… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”