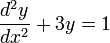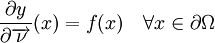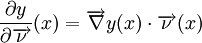Conditions aux limites de Neumann

En mathématiques, une condition aux limites de Neumann (nommée d'après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l'on spécifie les valeurs des dérivées que la solution doit vérifier sur les frontières/limites du domaine.

Dans le cas d'une équation différentielle telle que :

$\frac{d^2y}{dx^2} + 3 y = 1$

sur l'intervalle $[0,1]$ , la condition aux limites de Neumann s'exprime par :

y'(0) = α 1

y'(1) = α 2

où $α 1$ et $α 2$ sont deux nombres donnés.

Pour une équation aux dérivées partielles sur un domaine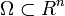 $\Omega\subset R^n$ telle que :

Δ y + y = 0

où $Δ$ exprime le Laplacien (opérateur différentiel), la condition aux limites de Neumann s'exprime par :

$\frac{\partial y}{\partial \overrightarrow{\nu}}(x) = f(x) \quad \forall x \in \partial\Omega$

où $f$ est une fonction connue définie sur la limite ∂Ω et à valeurs scalaires ; et 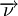$\overrightarrow{\nu}$ est le vecteur normal à la frontière ∂Ω. La dérivée normale dans le membre de gauche de l'équation, est définie par :

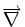$\frac{\partial y}{\partial \overrightarrow{\nu}}(x)=\overrightarrow{\nabla} y(x)\cdot \overrightarrow{\nu} (x)$

où $\overrightarrow{\nabla}$ est l'opérateur vectoriel de gradient, et le point marque le produit scalaire.

Voir aussi

La condition aux limites de Neumann est une condition qui apparaît naturellement dans les problèmes de transport. Il existe d'autres conditions possibles, par exemple les conditions aux limites de Dirichlet ou les conditions aux limites mixtes qui sont une combinaison des conditions de Neumann et Dirichlet.

Conditions aux limites
Conditions aux limites de Dirichlet
Conditions aux limites de Fourier ( ou Robin)
Conditions aux limites mixtes (mélées)

Portail des mathématiques

Ce document provient de « Conditions aux limites de Neumann ».

Catégorie : Conditions aux limites

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conditions aux limites de Neumann de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Conditions Aux Limites De Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Conditions aux limites de neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Conditions Aux Limites De Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Conditions aux limites de Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Conditions aux limites de dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Conditions aux limites — Condition aux limites Pour les articles homonymes, voir condition. En mathématiques, les conditions aux limites sont les valeurs que prennent les solutions des équations aux dérivées ordinaires et des équations aux dérivées partielles sur une… … Wikipédia en Français
Condition aux limites de Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Condition aux limites de Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Condition aux limites — Pour les articles homonymes, voir condition. En mathématiques, une condition aux limites est une contrainte sur les valeurs que prennent les solutions des équations aux dérivées ordinaires et des équations aux dérivées partielles sur une… … Wikipédia en Français
Condition aux limites de Robin — En mathématique, une condition aux limites de Robin (ou de troisième type) est un type de condition aux limites portant le nom du mathématicien français Victor Gustave Robin (1855 1897), qui a travaillé dans le domaine de la thermodynamique[1].… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Conditions aux limites de Neumann