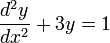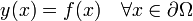Conditions aux limites de dirichlet

Conditions aux limites de Dirichlet

En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l'on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.

Dans le cas d'une équation différentielle telle que

$\frac{d^2y}{dx^2} + 3 y = 1$

sur l'intervalle $[0,1]$ la condition aux limites de Dirichlet s'exprime par :

y (0) = α 1

y (1) = α 2

où $α 1$ et $α 2$ sont deux nombres donnés.

Pour une équation aux dérivées partielles sur un domaine 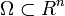$\Omega\subset R^n$ telle que

Δ y + y = 0

(où $Δ$ exprime le Laplacien), la condition aux limites de Dirichlet s'exprime par :

$y(x) = f(x) \quad \forall x \in \partial\Omega$

où $f$ est une fonction connue définie sur la limite ∂Ω.

La condition aux limites de Dirichlet est sans doute l'une des conditions aux limites les plus faciles à comprendre, mais il existe d'autres conditions possibles. Par exemple les conditions aux limites de Neumann ou les conditions aux limites mixtes qui sont une combinaison des conditions de Neumann et Dirichlet.

Portail des mathématiques

Ce document provient de « Conditions aux limites de Dirichlet ».

Catégorie : Conditions aux limites

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conditions aux limites de dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Conditions Aux Limites De Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Conditions aux limites de Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Conditions Aux Limites De Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Conditions aux limites de Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Conditions aux limites de neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français
Conditions aux limites — Condition aux limites Pour les articles homonymes, voir condition. En mathématiques, les conditions aux limites sont les valeurs que prennent les solutions des équations aux dérivées ordinaires et des équations aux dérivées partielles sur une… … Wikipédia en Français
Condition aux limites de Dirichlet — En mathématiques, une condition aux limites de Dirichlet est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs que la solution doit vérifier sur les frontières/limites du domaine.… … Wikipédia en Français
Condition aux limites — Pour les articles homonymes, voir condition. En mathématiques, une condition aux limites est une contrainte sur les valeurs que prennent les solutions des équations aux dérivées ordinaires et des équations aux dérivées partielles sur une… … Wikipédia en Français
Condition Aux Limites — Pour les articles homonymes, voir condition. En mathématiques, les conditions aux limites sont les valeurs que prennent les solutions des équations aux dérivées ordinaires et des équations aux dérivées partielles sur une frontière. Il existe un… … Wikipédia en Français
Condition aux limites de Neumann — En mathématiques, une condition aux limites de Neumann (nommée d après Carl Neumann) est imposée à une équation différentielle ou à une équation aux dérivées partielles lorsque l on spécifie les valeurs des dérivées que la solution doit vérifier… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Conditions aux limites de dirichlet