Cohomologie De Dolbeault

Cohomologie De Dolbeault: Cohomologie de Dolbeault

En géométrie complexe et en géométrie différentielle, la cohomologie de Dolbeault est une généralisation aux variétés complexes de la cohomologie de De Rham.

Définition du complexe de cochaines

Pour un fibré vectoriel holomorphe $E$ sur une variété complexe $M$ , les formes différentielles sur $M$ à valeurs dans $E$ se définissent comme les sections du fibré 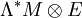$\Lambda^*M\otimes E$ . Parmi ces formes différentielles se distinguent celles qui sont linéaires en les $p$ premières variables et antilinéaires en les $q$ suivantes, dites de bidegré $(p, q)$ . On note usuellement $Ω p, q (M, E)$ l'espace vectoriel complexe des formes différentielles de bidegré $(p, q)$ à valeurs dans $E$ . Ces espaces sont en somme orthogonale et :
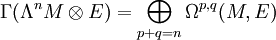$\Gamma(\Lambda^nM\otimes E)=\bigoplus_{p+q=n}\Omega^{p,q}(M,E)$ .
Si $E$ est le fibré en droites complexes trivial sur $M$ , on s'empresse de l'oublier dans les notations. En particulier :
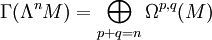$\Gamma(\Lambda^nM)=\bigoplus_{p+q=n}\Omega^{p,q}(M)$ .
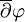Pour une forme différentielle $\varphi$ de bidegré (p,q), on note $\overline{\partial}\varphi$ la partie de degré $(p, q + 1)$ de 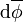$\mathrm d\overline{\phi}$ suivant la décomposition ci-dessus. Si $ξ$ est une section holomorphe (locale) de $E$ , alors 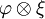$\varphi\otimes \xi$ définit une forme différentielle de bidegré $(p, q)$ à valeurs dans $E$ , et on définit :
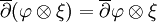$\overline{\partial}(\varphi\otimes \xi)=\overline{\partial}\varphi\otimes \xi$ .
Comme $E$ est localement engendré par ses sections holomorphes, 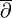$\overline{\partial}$ se prolonge en un opérateur sur $Ω p, q (M, E)$ à valeurs dans $Ω p, q + 1 (M, E)$ , appelé opérateur de Cauchy-Riemann. L'expression ci-dessus ne reste valable que pour des sections holomorphes de $E$ . On dispose donc de flèches :
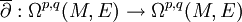$\overline{\partial}:\Omega^{p,q}(M,E)\rightarrow \Omega^{p,q}(M,E)$ .
Comme 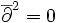$\overline{\partial}^2=0$ , on dispose d'un complexe de cochaines 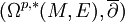$(\Omega^{p,*}(M,E),\overline{\partial})$ , dont le $q$ -ième groupe de cohomologie est appelé $(p, q)$ -groupe de Dolbeault :
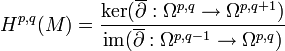$H^{p,q}(M)=\frac{\ker(\overline{\partial}:\Omega^{p,q}\rightarrow \Omega^{p,q+1})}{\operatorname{im}(\overline{\partial}:\Omega^{p,q-1}\rightarrow \Omega^{p,q}) }$ .
Théorème de Dolbeault

Le théorème de De Rham affirme que les complexes de De Rham et les complexes de cohomologie singulière d'une variété différentielle réelle sont homotopes. Le théorème de Dolbeault peut être vu comme un analogue complexe.

Théorème de Dolbeault — Le $(p, q)$ -ième groupe de cohomologie de Dolbeault du fibré holomorphe $E$ est canoniquement isomorphe au $q$ -ième groupe de cohomologie de Cech du faisceau des $p$ -formes holomorphes sur $M$ à valeurs dans $E$ :
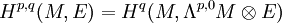$H^{p,q}(M,E)=H^q(M,\Lambda^{p,0}M\otimes E)$

Preuve

Dans l'identité ci-dessus, 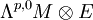$\Lambda^{p,0}M\otimes E$ , qui est un fibré holomorphe sur $M$ , est identifié au faisceau de ses sections holomorphes. On introduit 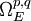$\Omega^{p,q}_E$ le faisceau des formes différentielles de bidegré $(p, q)$ à valeurs dans $E$ . Le lemme de Poincaré permet d'affirmer que la suite suivante est une suite exacte de faisceaux :
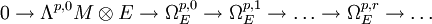$0\rightarrow \Lambda^{p,0}M\otimes E \rightarrow \Omega^{p,0}_E\rightarrow \Omega^{p,1}_E\rightarrow \dots\rightarrow \Omega^{p,r}_E\rightarrow\dots$ .
L'exactitude signifie dans la situation présente que les suites correspondantes des espaces des sections globales sur les ouverts contractibles sont des suites exactes d'espaces vectoriels. Cela ne signifie en aucun cas que la suite des espaces des sections globales sur la variété soit exacte. En oubliant le premier terme, on dispose d'un complexe de cochaines :
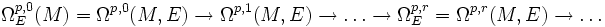
$\Omega^{p,0}_E(M)=\Omega^{p,0}(M,E)\rightarrow \Omega^{p,1}(M,E)\rightarrow\dots\rightarrow \Omega^{p,r}_E= \Omega^{p,r}(M,E)\rightarrow \dots$
qui n'est autre justement que le complexe définissant les groupes de cohomologie de Dolbeault. Le théorème de Dolbeault se déduit d'un résultat général en cohomologie de Cech concenant les résolutions acycliques. On donne ici une démonstration adaptée au cas étudié.

La suite exacte se scinde en des suites exactes courtes de faisceaux :
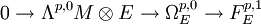$0\rightarrow \Lambda^{p,0}M\otimes E \rightarrow \Omega^{p,0}_E \rightarrow F^{p,1}_E$ et pour $r > 0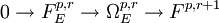$ , $0\rightarrow F^{p,r}_E\rightarrow \Omega^{p,r}_E\rightarrow F^{p,r+1}$
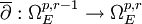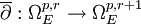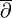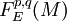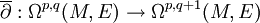où $F p, r$ désigne l'image de $\overline{\partial}:\Omega^{p,r-1}_E\rightarrow \Omega^{p,r}_E$ ou, par exactitude, le noyau de $\overline{\partial}:\Omega^{p,r}_E\rightarrow \Omega^{p,r+1}_E$ . De fait, c'est le faisceau des formes différentielles de bigré (p,q) à valeurs dans $E$ et $\overline{\partial}$ -fermées. Remarquons que $F^{p,q}_E(M)$ est exactement le noyau de $\overline{\partial}:\Omega^{p,q}(M,E)\rightarrow \Omega^{p,q+1}(M,E)$ . 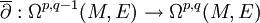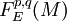L'image de $\overline{\partial}:\Omega^{p,q-1}(M,E)\rightarrow \Omega^{p,q}(M,E)$ est contenue dans $F^{p,q}_E(M)$ .

Ces suites exactes courtes induisent des suites exactes longues en cohomologie de Cech (qu'on se garde d'expliciter ici). Comme les faisceaux 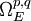$\Omega^{p,q}_E$ sont acycliques (existence de partitions de l'unité sur toute variété réelle), un terme sur quatre de cette suite exacte longue est nulle. Les morphismes de bord apparaissent presque tous comme des isomorphismes, ce qui donne les identités suivantes :

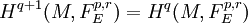Pour $q > 0$ , et $r > 0$ , $H^{q+1}(M,F^{p,r}_E)=H^q(M,F^{p,r}_E)$ ;

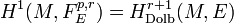Pour $r > 0$ , $H^1(M,F^{p,r}_E)=H^{r+1}_{\rm Dolb}(M,E)$ ;

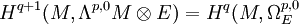Pour $q > 0$ , $H^{q+1}(M,\Lambda^{p,0}M\otimes E)=H^q(M,\Omega^{p,0}_E$ ;

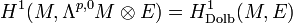Puis $H^1(M,\Lambda^{p,0}M\otimes E)=H^1_{\rm Dolb}(M,E)$ ;

Et enfin $H^0(M,\Lambda^{p,0}M\otimes E)=\ker\left[\overline{\partial}:\Omega^{p,0}_E(M)\rightarrow F^{p,1}_E(M)\right]= H^0_{\rm Dolb}(M,E)$ .

La combinaison de ces isomorphismes fournit le résultat recherché. La naturalité (ou fonctorialité) des isomorphes obtenus découle immédiatement des propriétés de fonctorialité des suites exactes longues de groupes de cohomologie de Cech en fonction des suites exactes courtes. La démonstration du théorème de Dolbeault est terminée.

Portail des mathématiques

Ce document provient de « Cohomologie de Dolbeault ».

Catégories : Théorie d'homologie | Géométrie complexe | Topologie différentielle | Forme différentielle

Contenu soumis à la licence CC-BY-SA. Source : Article Cohomologie De Dolbeault de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Cohomologie de dolbeault — En géométrie complexe et en géométrie différentielle, la cohomologie de Dolbeault est une généralisation aux variétés complexes de la cohomologie de De Rham. Définition du complexe de cochaines Pour un fibré vectoriel holomorphe E sur une variété … Wikipédia en Français
Cohomologie de Dolbeault — En géométrie complexe et en géométrie différentielle, la cohomologie de Dolbeault (de) est une généralisation aux variétés complexes de la cohomologie de De Rham. Définition du complexe de cochaines Pour un fibré vectoriel holomorphe E sur… … Wikipédia en Français
Cohomologie De De Rham — En mathématiques, la cohomologie de de Rham est un outil de topologie différentielle, c est à dire adapté à l étude des variétés différentielles. Il s agit d une théorie cohomologique basée sur des propriétés algébriques des espaces de formes… … Wikipédia en Français
Cohomologie de de rham — En mathématiques, la cohomologie de de Rham est un outil de topologie différentielle, c est à dire adapté à l étude des variétés différentielles. Il s agit d une théorie cohomologique basée sur des propriétés algébriques des espaces de formes… … Wikipédia en Français
Cohomologie de De Rham — En mathématiques, la cohomologie de De Rham est un outil de topologie différentielle, c est à dire adapté à l étude des variétés différentielles. Il s agit d une théorie cohomologique basée sur des propriétés algébriques des espaces de formes… … Wikipédia en Français
Dolbeault-Kohomologie — Die Dolbeault Kohomologie ist ein mathematisches Objekt aus dem Bereich der Differentialtopologie und der komplexen Geometrie. Benannt wurde es nach dem Mathematiker Pierre Dolbeault, der das Objekt 1953 definierte und untersuchte. Die Dolbeault… … Deutsch Wikipedia
Dolbeault cohomology — In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology (named after Pierre Dolbeault) is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold. Then the Dolbeault… … Wikipedia
Théorème de dualité de De Rham — Cohomologie de De Rham En mathématiques, la cohomologie de de Rham est un outil de topologie différentielle, c est à dire adapté à l étude des variétés différentielles. Il s agit d une théorie cohomologique basée sur des propriétés algébriques… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts