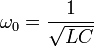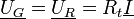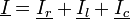- Circuit RLC série
-
Circuit RLC
En électrocinétique, un circuit RLC est un circuit linéaire contenant une résistance électrique, une bobine (inductance) et un condensateur (capacité).
Il existe deux types de circuits RLC série ou parallèle, selon l'interconnexion des trois types de composants. Le comportement d'un circuit RLC est généralement décrit par une équation différentielle du second ordre (là où des circuits RL ou circuits RC se comportent comme des circuits du premier ordre).
À l'aide d'un générateur de signaux, il est possible d'injecter dans le circuit des oscillations et observer dans certains cas une résonance, caractérisée par une augmentation du courant (lorsque le signal d'entrée choisi correspond à la pulsation propre du circuit, calculable à partir de l'équation différentielle qui le régit).
Sommaire
Circuit RLC en série
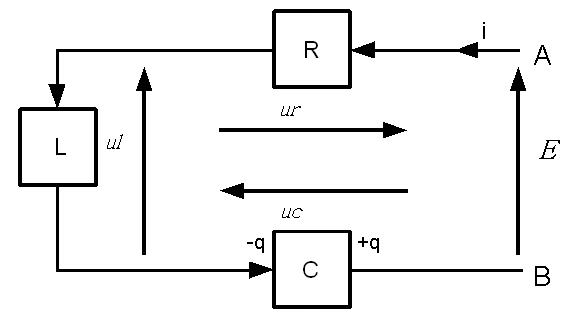
Circuit soumis à un échelon de tension
Si un circuit RLC série est soumis à un échelon de tension
 , la loi des mailles impose la relation :
, la loi des mailles impose la relation :En introduisant la relation caractéristique du condensateur :
on obtient l'équation différentielle du second ordre :
Avec :
- E la force électromotrice du générateur, en volts (V) ;
- uC la tension aux bornes du condensateur, en volts (V) ;
- L l'inductance de la bobine, en henrys (H) ;
- i l'intensité du courant électrique dans le circuit, en ampères (A) ;
- q la charge électrique du condensateur, en coulombs (C) ;
- C la capacité électrique du condensateur, en farads (F) ;
- Rt la résistance totale du circuit, en ohms (Ω) ;
- t le temps en secondes (s)
Dans le cas d'un régime sans pertes, c’est-à-dire pour
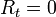 , on obtient une solution se mettant sous la forme :
, on obtient une solution se mettant sous la forme :Avec :
- T0 la période d'oscillation, en secondes ;
- φ la phase à l'origine (le plus souvent choisie telle que φ = 0)
Circuit soumis à une tension sinusoïdale
La transformation complexe appliquée aux différentes tensions permet d'écrire la loi des mailles sous la forme :
soit, en introduisant les impédances complexes :
La fréquence angulaire de résonance en intensité d'un tel circuit ω0 est donnée par :
Pour cette fréquence la relation ci-dessus devient :
et on a :
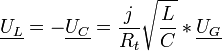
Circuit RLC en parallèle
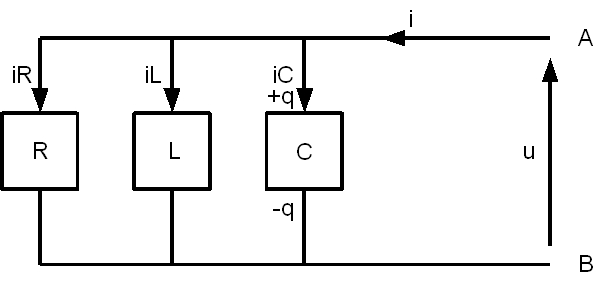
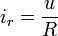
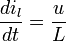
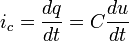
car q = Cu
i = ir + il + ic
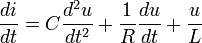
Attention : la branche C est en court-circuit : on ne peut pas brancher A, B directement aux bornes d'un générateur E, il faut lui ajouter une résistance.
Les deux conditions initiales sont :
- il0 garde sa valeur avant la mise sous tension (car l'inductance s'oppose à la variation du courant).
- q0 garde sa valeur avant la mise sous tension
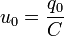 .
.
Circuit soumis à une tension sinusoïdale
La transformation complexe appliquée aux différentes intensités donne :
soit, en introduisant les impédances complexes :
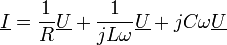
- soit :
![\underline I = \left[ \frac{1}{R} + j (C \omega - \frac{1}{L \omega}) \right] \underline U](/pictures/frwiki/56/8640a8358611b48e02390533687a5b8d.png)
La fréquence angulaire de résonance en intensité d'un tel circuit ω0 est donnée par :
Pour cette fréquence la relation ci-dessus devient :
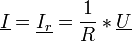
- et on a :
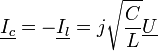
Voir aussi
Liens externes
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégories : Systèmes oscillants | Circuit électrique
Wikimedia Foundation. 2010.

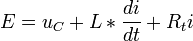
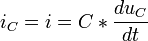
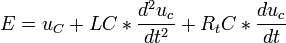
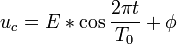
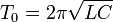
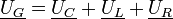
![\underline {U_G} = - \frac{j}{C \omega} \underline I + j L \omega \underline I + R_{t} * \underline I = \bigg[ R_t + j \frac{LC \omega^2 - 1}{C \omega} \bigg] \underline I](/pictures/frwiki/48/06d577c31533e503b726f54e76fce31d.png)