- Chute libre (cinematique)
-
Chute libre (cinématique)
 Pour les articles homonymes, voir Chute libre.
Pour les articles homonymes, voir Chute libre.
La cinématique de la chute libre est déterminée par la formule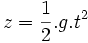 de Galilée (1564-1642).
de Galilée (1564-1642).Sommaire
Historique
Cette formule n'a pas été découverte en un jour. Historiquement, on la trouve chez Domingo de Soto, mais c'est pure spéculation. Benedetti prépare Galilée et le de Motu de Buonamico Buffalmacco est étudié à Pise par Galilée, qui écrit dès 1590. La loi est énoncée dès 1604 (lettre à Fra Paolo Sarpi), mais via une double erreur. Puis la démonstration est corrigée dans le Dialogo (1630). Cavalieri (1632) et Mersenne (1633) en tirent la chute parabolique avec vitesse initiale horizontale. Torricelli trouvera enfin la parabole de sûreté.
Rappel de la démonstration
On considère un corps de masse m soumis au champ de pesanteur
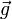 terrestre.
terrestre.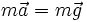 où
où 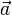 est l'accélération du corps. Donc
est l'accélération du corps. Donc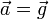 (m se simplifie : constaté et affirmé par Galilée).
(m se simplifie : constaté et affirmé par Galilée).- On intègre une fois, par rapport au temps :
v = g.t + cste où v est la vitesse verticale.
Si la vitesse initiale est nulle alors v = g.t.
Cette loi est énoncée par Galilée, au grand dam de ceux qui pensent que si la vitesse initiale est nulle, le mobile ne peut avancer !
- On intègre encore une fois par rapport au temps :
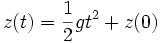 .
.
On obtient ainsi le mouvement d'un corps en chute libre.
Application numérique avec rappel des unités
On peut remarquer que :
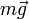 est une force, la force de pesanteur ou poids en newton (N). Donc g est en N/kg , c'est-à-dire en m/s2.
est une force, la force de pesanteur ou poids en newton (N). Donc g est en N/kg , c'est-à-dire en m/s2.- Sa valeur à la surface de la terre est 9 81 N/kg à 45° de latitude. Ainsi, nous aurions les données suivantes avec, pour faire simple, 10 N/kg :
Durée Vitesse en m/s Vitesse en km/h Distance de chute 1 s 10 m/s 36 km/h 5 m 2 s 20 m/s 72 km/h 20 m 5 s 50 m/s 180 km/h 125 m - Suite à une question de Beeckman à Descartes (avant 1629), si le mobile descend de h dans le temps t1, le temps t2 qu'il mettra pour descendre encore de h est :
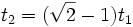
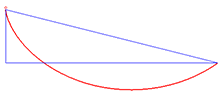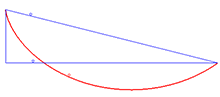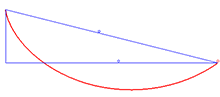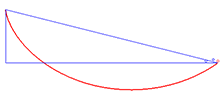 Courbe brachistochrone
Courbe brachistochrone- Un problème classique du XVIIe siècle : soit le triangle égyptien AOB rectangle en O ; OA =3a vertical et OB = 4a horizontal : une masse M1 glisse sans frottement sur le parcours AOB (alésé en O), l'autre masse M2 glisse sans frottement selon AB : laquelle arrive la première ? Réponse : si OA est plus grand, M2 arrive en tête (voir cycloïde).
Et Galilée ?
Du temps de Galilée, on ne connaissait ni les dérivées, ni la théorie de Newton, ni les unités. C'est juste après lui qu'on effleure le problème. De même qu'on ne divise pas un vecteur par un vecteur, il était idiot, à l'époque, de diviser une distance par un temps.
Il s'est en fait contenté de dire que la vitesse augmentait comme 0+1 , 1+2 , 2+3 , 3+4 , etc., c'est-à-dire 1,3,5,7,... dans des temps égaux : ceci veut dire v = g.t dans notre langage.
Affirmer qu'il l'a constaté expérimentalement est "plutôt douteux" (cf ci-après Expérimentation).
Cependant, c'était un excellent théoricien, il eût pu raisonner ainsi (mais on n'en a pas trace) :
- Soit f(t1) la vitesse atteinte au temps t1 (ou sa valeur moyenne, peu importe). Alors on doit avoir d'après le principe de relativité : f(t1) + f(t2 − t1) = f(t2).
- Prenons t2 = 2t1, c'est-à-dire f(2t1) = 2f(t1). Et plus généralement f(n.t) = nf(t).
- Donc la vitesse au temps n.t est n fois plus grande que la vitesse au temps t.
Il raisonnait sans doute avec la vitesse moyenne entre deux temps, car il dit 1+2, 2+3, etc., mais le raisonnement reste exact. En fait il raisonnait en termes de chemin parcouru : il est clair que
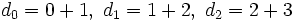 , et bien sûr, via la somme des n premiers impairs : 1+ 3 + 5 +... = n² (raisonnement connu depuis très longtemps), il retrouvait z proportionnel à n².
, et bien sûr, via la somme des n premiers impairs : 1+ 3 + 5 +... = n² (raisonnement connu depuis très longtemps), il retrouvait z proportionnel à n².Pour réaliser une expérience, encore fallait-il qu'il possédât une montre qui donne la cadence. Dugas (histoire de la mécanique) indique que c'est avec une clepsydre (pour le cas du plan incliné) qu'il pouvait faire cette mesure ; il pesait une masse d'eau coulant à débit constant ; auparavant il utilisait la cadence du chant (son père était un musicien réputé).
- Remarque : il aurait pu aussi faire cette expérimentation : soit t1 ; t2 =t1+t et t3 =t1+2t, trois temps consécutifs, où l'on marque z1, z2, z3. Alors, on peut vérifier 2.z2 - (z1 + z3) = constante indépendante de t1 et valant toujours g.t^2 car 2.(t1+t)^2 - [t1^2 +(t1+2t)^2] = 2 .t^2. On peut montrer que ceci est caractéristique de z ~ t^2.
Quoi qu'il en soit, la notion de force de pesanteur n'est pas claire. Chez Torricelli qui manipule mieux le calcul infinitésimal, certaines expressions sont très modernes.
La Tour de Pise
Jamais une balle de plume et une balle de plomb ne tombent selon la même loi de chute en raison de la résistance de l'air.
Galilée le sait bien, puisqu'il en discute dans son de Motu, écrit à Pise vers 1591. C'est dans les années passées à Pise qu'il se détache de la Scolastique, mais c'est seulement vers 1604, à Padoue, qu'il possède le fameux z = t2, via une double erreur de raisonnement[1].
Et il n'y a pas eu de vérification expérimentale faite depuis la Tour : c'est une légende, un peu comme la pomme de Newton : voir l'article célèbre de Koyré qui ridiculise cette légende[2].
Article détaillé : chute avec résistance de l'air.Expérimentation réaliste
On montre assez vite que sur un plan incliné d'angle A, seule la composante, selon le plan, de la pesanteur intervient : la chute est ralentie d'un facteur sinA[3].
En prenant A suffisamment faible, par exemple, sinA = 1 / 100, alors le temps pour parcourir 1 mètre est de 4,47 s : il est possible de pointer z1, z2 et z3 chaque seconde, avec assez de précision. Mais il faut éviter le frottement ; ou bien faire rouler une bille, sans glissement : on montre qu'il faut tenir compte d'un facteur (1/(1+2/5)) = 5/7 (voir roulement sur un plan incliné). Mais à ceci près, on peut vérifier que la distance parcourue est bien z~ t^2. Très astucieusement on raboutait un plan incliné d'angle B (en alésant soigneusement la jointure) ; et Galilée et Torricelli avaient compris que la bille remontait à la même hauteur et que les temps étaient comme racine carrée (1 / sinB).
D'ailleurs Galilée avait vite compris que lorsqu'un pendule oscillait, ce qui se passait à gauche était identique à ce qui se passait à droite. Et il l'interprétait à juste titre comme un mouvement sur une succession de plans inclinés (cf pendule cycloïdal et pendule simple). La conclusion était alors patente : la période T était proportionnelle à sqrt(l). Mais il ne l'énonça pas tout de suite.
Par contre,
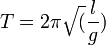 viendra plus tard avec Torricelli et Huygens.
viendra plus tard avec Torricelli et Huygens.Suite à l'analyse critique de Koyré[4], on s'est pris à douter de la réalité des expériences de Galilée, leur réservant le sort de gedanken experiments. Il fallut l'intervention de Stillman Drake (1979)[5], pour que l'on retrouve les notes de travaux pratiques de Galilée.
TP récent
Les élèves laissent tomber un cylindre vertical gradué très lourd. Des cellules photoélectriques indiquent le passage des encoches A, B, C, D.
Ou bien trois photos sont prises aux temps t1, t2 = t1 + t et t3 = t1 + 2t. On fait les calculs 2.z2 -(z1+z3) pour les 4 points A, B, C, D et on prend la moyenne : c'est g.t^2. On fait varier t1 : rien ne change (ou presque). On fait varier t, et on porte g.t^2 en fonction de t^2. La valeur de g, on s'en doute, est approchée par défaut : il reste toujours la résistance de l'air !
Les élèves sont déçus, sauf si on fait une évaluation extrapolée quand t diminue, puis quand t1 diminue : certes leur valeur n'est pas exacte, mais... le "must" est de faire remarquer que les valeurs de g diminuent assez systématiquement si t1 augmente. Et qu'au fond, dans le cours laps de temps 2t, l'accélération était g - av^2 = g- B.t1^2. Ils se précipitent à nouveau sur leurs résultats. Grosse joie et gros dépit : c'est bien meilleur, mais quand même la dispersion des résultats d'une classe est incontestable : on n'arrivera pas à 4 chiffres significatifs. Le pendule de Kater restera inégalé avec 5 chiffres significatifs, pendant plus d'un siècle (cf chute avec résistance de l'air).
Méthode de Sakuma (1970, au BIPM)
Très jolie manipulation, à juste titre récompensée : on fait tomber, dans le vide, le miroir d'un interféromètre de Michelson, et on enregistre le défilement des franges. Bien sûr, petite astuce technologique, le miroir est un coin de cube, c'est dire que peu importe son orientation. On a essayé le catapultage vers le haut et redescente, mais finalement, ce n'est pas tellement meilleur.
La précision actuelle est de 5 microgals (1 gal = 10-5 m/s2). On voit parfaitement la force de marée luni-solaire (100 microgals) qui est une composante du poids, variable, souvent négligée (cf. pesanteur). Un exemple sur eost.u-strasbg.fr.
Précautions à prendre
Dès que l'on cherche cette précision avec 12 chiffres significatifs, il faut faire très attention à ce que l'on écrit : g, à cette précision de 12 chiffres significatifs, varie vite avec l'altitude h de la mesure ; chaque variation de R/2. 10(-12) = 3.2 micromètres se voit !
Donc, en réalité, on mesure une valeur de g intermédiaire : on doit appliquer les formules de Kepler, ce qui est impressionnant ! Soit g en O et g.(1 + h / R)2 au point A de chute : quel est le point B intermédiaire où l'expérience évalue g ?
Newton a traité ce problème : Soit TO = R = 2a et TA = a(1+cosθ), le temps de chute rigoureux, depuis le périgée O est t/T = θ + sinθ ; ce qui conduit au résultat exact. Par approximation, on trouve le point B tel que OB = OA/6 , à mieux que 10^(-12) près.
Au plateau de Calern[6], on voit la dilatation annuelle du plateau de Calern (la correction de Bouguer reste la même, mais pas celle de Faye) : c'est dire la sophistication des mesures depuis Galilée.
Enfin, il faut veiller à ne point approcher par dessus ou dessous des masses trop importantes. A contrario, le faire permet de mesurer la constante de gravitation G (cf expérience de Cavendish).
Notes et références
- ↑ lettre à Paolo Sarpi
- ↑ Koyré, Annales de l'Université de Paris, 1937 ; article reproduit in : Koyré, "Études d'histoire de la pensée scientifique", PUF, 1966)
- ↑ c'est la célèbre Loi des cordes du cercle de Galilée, 1602.
- ↑ cf Études galiléennes
- ↑ Repris dans son livre, Galileo : pioneer scientist, University of Toronto Press, 1990, (ISBN 0802027253).
- ↑ OCA, Observatoire de la Côte d'Azur
Voir aussi
- Chute libre
- Chute avec résistance de l'air
- Roulement sur un plan incliné
- Énergie potentielle (gravitationnelle)
- Portail de la physique
Catégories : Article à désacadémiser | Dynamique du solide
Wikimedia Foundation. 2010.
