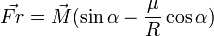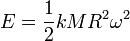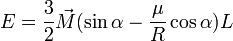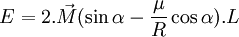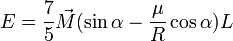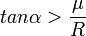Roulement sur un plan incline

Roulement sur un plan incliné

Soit un corps cylindrique de masse 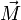$\vec{M}$ (kg), de centre de gravité $G$ , de rayon $R$ (m), roulant sans glisser sur un plan incliné d’un angle $α$ avec l’horizontale, à une vitesse de translation $V$ (m/s) et de rotation $ω$ (rad/s), le coefficient de résistance au roulement est $μ$ .

Ce corps cylindrique engendre des actions statiques dues à sa masse et des réactions du plan sur lequel il repose.
En mouvement, ce corps engendre des actions dynamiques qui lui sont propres et un couple résistant au roulement dû au contact avec le plan incliné sur lequel il se déplace.

Actions statiques

Actions du corps sur le plan

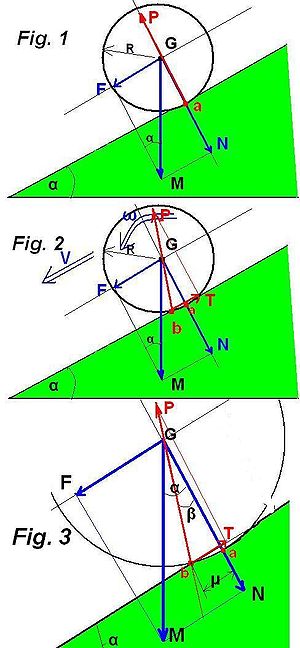
La fig.1 représente la décomposition de 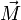$\vec{M}$ en deux composantes : la composante 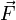$\vec{F}$ parallèle au plan, la force 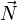$\vec{N}$ normale au plan au point de contact « a » et la réaction 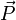$\vec{P}$ du plan.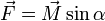

$\vec{F} = \vec{M}\sin\alpha$

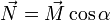
$\vec{N} = \vec{M}\cos\alpha$

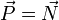$\vec{P} = \vec{N}$ .

Réactions du plan

Dans la figure 3, le plan s’oppose au roulement selon une force 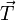$\vec{T}$ qui est la réaction du plan, dont le coéfficient de résistance au roulement est $μ$ .

Le couple résistant sera 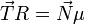$\vec{T} R = \vec{N} \mu$ , comme 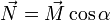$\vec{N} = \vec{M} \cos\alpha$ , nous aurons :

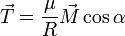$\vec{T}=\frac{\mu}{R} \vec{M}\cos\alpha$ ,

force qui s’oppose à $\vec{F}$ .

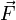Force résultante

La force résultante qui fait rouler le corps sera 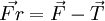$\vec{Fr}=\vec{F}-\vec{T}$ et comme 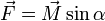$\vec{F}=\vec{M}\sin\alpha$ , nous obtenons

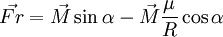$\vec{Fr}=\vec{M}\sin\alpha-\vec{M}\frac{\mu}{R}\cos\alpha$ ,

et en simplifiant :

$\vec{Fr}=\vec{M}(\sin\alpha-\frac{\mu}{R}\cos\alpha)$

Actions dynamiques

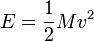
Énergie cinétique de translation: c’est l’énergie produite par le corps qui se déplace par rapport à un plan (en joules).; $E=\frac{1}{2} M v^2$

Énergie cinétique de rotation: c’est l’énergie produite par la rotation d’un corps autour d’un axe (le plus souvent passant par son centre de gravité).

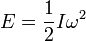$E=\frac{1}{2} I \omega ^2$ , avec le moment d’inertie $I = k M R 2$ , où k est un coefficient qui dépend de la forme du corps. En remplaçant $I$ par sa valeur, nous obtenons :

$E=\frac{1}{2} k M R^2 \omega ^2$

Énergie cinétique totale produite: c’est la somme des deux énergies précédentes.

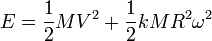$E=\frac{1}{2} M V^2 + \frac{1}{2} k M R^2 \omega ^2$ et comme $V 2 = R 2 ω 2$ , nous obtenons :

$E=(\frac{1}{2}+\frac{1}{2} k) M V^2$

En remplaçant k par sa valeur en fonction du corps nous obtenons (k=1/2 pour un disque plein, k=1 pour une jante et k=2/5 pour une sphère), et comme 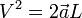$V^2=2 \vec{a} L$ , où $L$ est la distance parcourue par le corps, 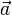$\vec{a}$ est l’accélération prise par le corps = 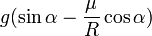$g(\sin\alpha-\frac{\mu}{R}\cos\alpha)$ , nous aurons pour les 3 corps différents :

pour un disque plein (k=1/2), 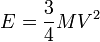, soit:
- $E=\frac{3}{2}\vec{M}(\sin\alpha-\frac{\mu}{R}\cos\alpha) L$
pour une jante (k=1), E = MV², soit :
- $E=2.\vec{M}(\sin\alpha-\frac{\mu}{R}\cos\alpha).L$
pour une sphère (k=2/5), 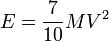, soit :
- $E=\frac{7}{5}\vec{M}(\sin\alpha-\frac{\mu}{R}\cos\alpha) L$

Condition de roulement

Pour qu’il y ait mouvement: pour qu’il y ait mouvement le couple moteur 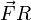$\vec{F} R$ doit être supérieur au couple résistant :

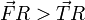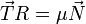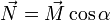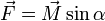$\vec{F} R > \vec{T} R$ comme $\vec{T} R= \mu \vec{N}$ , que $\vec{N}=\vec{M} \cos\alpha$ et $\vec{F}=\vec{M} \sin\alpha$ , nous aurons :

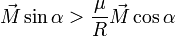$\vec{M} \sin\alpha > \frac{\mu}{R} \vec{M} \cos\alpha$ et en simplifiant :

$tan\alpha >\frac{\mu}{R}$

Pour qu’il n’y ait pas glissement: il n’y aura pas de glissement tant que 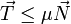$\vec{T}\le\mu \vec{N}$ , d’après la loi du frottement de Coulomb.

$\vec{T}$ dépend également de la forme

k

des corps.

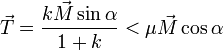$\vec{T}=\frac{k \vec{M} \sin\alpha}{1+k} < \mu \vec{M} \cos\alpha$ , d’où :

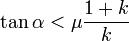
$\tan\alpha < \mu \frac{1+k}{k}$

Articles connexes

Portail de la physique

Ce document provient de « Roulement sur un plan inclin%C3%A9 ».

Catégorie : Mécanique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Roulement sur un plan incline de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Roulement sur un plan incliné — Soit un corps cylindrique de masse (kg), de centre de gravité G, de rayon R (m), roulant sans glisser sur un plan incliné d’un angle α avec l’horizontale, à une vitesse de translation V (m/s) et de rotation ω (rad/s), le coefficient de résistance … Wikipédia en Français
Plan incline — Plan incliné Légende : N = Force normale qui est perpendiculaire au plan m = la masse de l objet g = l accélération due à la gravité θ (theta) = Angle d inclinaison du plan, (mesuré par rapport au plan horizontal) f = force de frottement du… … Wikipédia en Français
Plan incliné — Légende : N = Force normale qui est perpendiculaire au plan m = la masse de l objet g = l accélération due à la gravité θ (theta) = Angle d inclinaison du plan, (mesuré par rapport au plan horizontal) f = force de frottement du plan incliné… … Wikipédia en Français
Luge sur rail — Pour les articles homonymes, voir Luge. Eifel Coaster d Eifelpark, Allemagne … Wikipédia en Français
Chute Libre (Cinématique) — Pour les articles homonymes, voir Chute libre. La cinématique de la chute libre est déterminée par la formule de Galilée (1564 1642). Sommaire 1 Historique … Wikipédia en Français
Chute libre, cinématique — Chute libre (cinématique) Pour les articles homonymes, voir Chute libre. La cinématique de la chute libre est déterminée par la formule de Galilée (1564 1642). Sommaire 1 Historique … Wikipédia en Français
Chute libre (cinematique) — Chute libre (cinématique) Pour les articles homonymes, voir Chute libre. La cinématique de la chute libre est déterminée par la formule de Galilée (1564 1642). Sommaire 1 Historique … Wikipédia en Français
lancement — [ lɑ̃smɑ̃ ] n. m. • 1306, repris XIXe; de 1. lancer 1 ♦ Action de lancer, de projeter. Lancement du disque, du javelot. ⇒ 2. lancer. Le lancement d une grenade à main. Spécialt Projection au moyen d un dispositif de propulsion. Lancement d une… … Encyclopédie Universelle
Notion de module — Pour les articles homonymes, voir Module. Un module est une unité de mesure conventionnelle adoptée pour régler les diverses parties d un ensemble (construction, machine...). Il correspond à la plus petite commune mesure que doivent posséder les… … Wikipédia en Français
Compagnie des mines de Lens — Création 1849 Disparition 1946 (Nationalisation) Siège social … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Roulement sur un plan incline

Roulement sur un plan incliné

Sommaire