Catégorie monoïdale symétrique

Catégorie monoïdale symétrique

Catégorie monoïdale tressée

En mathématiques, une catégorie monoïdale tressée est une catégorie monoïdale particulière, à laquelle on ajoute l'analogue de la notion de commutativité.

Définition formelle

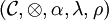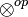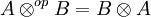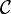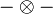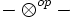Soit (\mathcal{C},\otimes,\alpha,\lambda,\rho) une catégorie monoïdale. On note \otimes^{op} le produit tensoriel opposé à \otimes, c'est-à-dire le bifoncteur défini par A \otimes^{op} B = B \otimes A. On appelle tressage sur \mathcal{C} un isomorphisme naturel β de -\otimes - vers - \otimes^{op}-. Autrement dit, pour tous objets A,B de 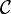\mathcal{C}, β induit un isomorphisme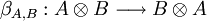

\beta_{A,B}: A \otimes B \longrightarrow B \otimes A

Représentation des groupes de tresses

Par définition, β induit aussi un isomorphisme 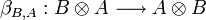\beta_{B,A}: B \otimes A \longrightarrow A \otimes B, qui peut etre inversé (puisque bijectif). Ceci induit donc un isomorphisme 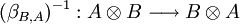(\beta_{B,A})^{-1}: A \otimes B \longrightarrow B \otimes A, qui en général est différent de βA,B.


Si V est un objet de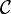 \mathcal{C}, quitte à fixer un parenthésage (puisque le produit tensoriel n'est associatif qu'à isomorphisme près), cela a un sens de considérer l'objet 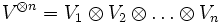V^{\otimes n}=V_1 \otimes V_2 \otimes \dots \otimes V_n. Puisque les Vi sont tous égaux à V, on a en particulier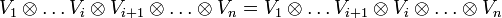

V_1\otimes \dots V_i \otimes V_{i+1} \otimes \dots \otimes V_n = V_1\otimes \dots V_{i+1} \otimes V_{i} \otimes \dots \otimes V_n

où il s'agit cette fois ci d'une véritable égalité et non d'un isomorphisme. Par ailleurs, β induit un isomorphisme

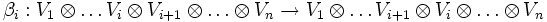
\beta_i:V_1\otimes \dots V_i \otimes V_{i+1} \otimes \dots \otimes V_n \rightarrow V_1\otimes \dots V_{i+1} \otimes V_{i} \otimes \dots \otimes V_n

Ainsi, les applications βi pour 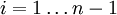i=1\dots n-1 peuvent être considérées comme des éléments du groupes des automorphismes de 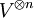V^{\otimes n}. On en déduit qu'il existe un morphisme de groupe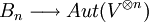

B_n \longrightarrow Aut(V^{\otimes n})

qui envoie σi sur βi.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Cat%C3%A9gorie mono%C3%AFdale tress%C3%A9e ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Catégorie monoïdale symétrique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Opérade — En algèbre générale, une opérade est une structure algébrique modélisant les propriétés (associativité, commutativité et autres relations) d une algèbre. Intuitivement, les éléments d une opérade correspondent à des opérations à plusieurs entrées …   Wikipédia en Français

  • Opérades — Opérade En algèbre générale, une opérade est une structure algébrique modélisant les propriétés (associativité, commutativité et autres relations) d une algèbre. Intuitivement, les éléments d une opérade correspondent à des opérations à plusieurs …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Tenseur (mathématiques) —  Pour l’article homonyme, voir Tenseur.  Les tenseurs sont des objets mathématiques issus de l algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs. On les rencontre notamment en analyse vectorielle et en… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”