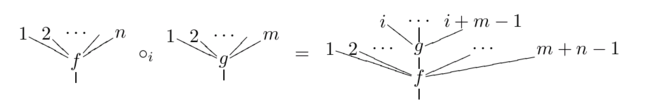Opérade

En algèbre générale, une opérade est une structure algébrique modélisant les propriétés (associativité, commutativité et autres relations) d'une algèbre. Intuitivement, les éléments d'une opérade correspondent à des opérations à plusieurs entrées, que l'on peut additionner et composer. On représente ces opérations par des arbres, que l'ont peut greffer les uns aux autres pour représenter les compositions. Les opérades ont été introduites en topologie algébrique par May, Boardman et Vogt au début des années 1970, notamment pour modéliser les espaces de lacets itérés.

Paradigme

Regardons la structure algébrique que l'on peut mettre sur les ensembles P(n) des fonctions à plusieurs variables de Vⁿ (pour tout entier n positif) dans V, où V est un espace vectoriel réel. On peut multiplier une fonction par un réel, et additionner deux fonctions de P(n). On a ainsi une structure d'espace vectoriel sur chaque P(n), donc une structure de module sur P(n). On peut rajouter une opération de composition, généralisant le classique existant pour les fonctions d'une variable : à f(x₁,...x_n) et g(y₁,...,y_m), on peut associer une fonction à n+m-1 variables f(x₁,...,g(y₁,...,y_m),...,x_n) où on a remplacé x_i par la fonction g. On note cette opération , et on l'appelle « produit de composition partiel » (de g à la ième place de f). On peut représenter graphiquement cette opération par une greffe d'arbres :

Ce produit de composition partiel vérifie deux relations d'associativité, correspondant au fait que l'ordre n'importe pas dans les compositions suivantes :

La suite des ensembles P(n), munie de ces opérations (multiplication par un scalaire, addition, produit de composition partiel), est une opérade non symétrique.

On peut faire agir le groupe symétrique Σ_n sur n variables et obtenir par équivariance une action de Σ_n sur chaque P(n). Cette action possède des propriétés de compatibilité avec les opérations de l'opérade. Ceci donne une structure d'opérade à la suite des ensembles P(n).

On peut définir un produit de composition (total) à partir du produit de composition partiel : on remplace toutes les variables des entrées de f par d'autres fonctions g_i. Ce produit est noté .

Définition d'une opérade

Une opérade non symétrique est une suite d'ensembles P(n) munie d'un produit de composition et d'un élément unité 1 dans P(1) tels que les propriétés d'associativité et d'unité sont vérifiées. L'associativité s'écrit de la façon suivante : .

L'axiome d'unité s'écrit : .

Une opérade est une opérade non symétrique telle que chaque P(n) est muni d'une action du groupe symétrique compatible avec les opérations de composition.

Remarque : Cette définition est dans le cadre de la catégorie des ensembles, mais une opérade est généralement définie pour une catégorie monoïdale symétrique quelconque. On travaille souvent aussi dans le cadre des modules (et les opérades sont alors dites opérades algébriques), ou dans le cadre des ensembles topologiques (on parle d'opérade topologique).

Définition d'algèbre sur une opérade

Pour une opérade algébrique, une algèbre sur une opérade est un module A muni d'une famille de morphismes .

Remarque : Cette notion est le lien entre algèbres et opérades.

Exemples

1. On peut associer une opérade à tout type d'algèbre. Par exemple, il existe une opérade associative (souvent notée As), les algèbres sur cette opérade étant les algèbres associatives. Il existe de même une opérade commutative (notée Com, et les algèbres sur cette opérade sont les algèbres commutatives), une opérade de Lie (notée Lie), etc.
2. Comme pour de nombreuses structures algébriques, il existe la notion d'objet libre. L'opérade libre est fréquemment utilisée pour définir des opérades par générateurs et relations. Par exemple, l'opérade associative est définie comme l'opérade libre sur un unique générateur quotientée par l'idéal engendré par la relation d'associativité.
3. Pour A une algèbre, on peut définir une opérade P où P(1) = A et P(n) = 0 sinon. Ceci montre que toute algèbre peut être vue comme une opérade (ce lien est différent du lien donné par les algèbres sur les opérades).
4. L'opérade (topologique) des petits disques (ou petits cubes) est un exemple important. Elle vient de la théorie de l'homotopie. Intuitivement, un élément de P(n) correspond à l'arrangement de n petits disques dans le disque unité, et la composition de deux éléments revient à insérer les petits disques de l'un dans un petit disque de l'autre.

Origines du mot

Le mot opérade (operad en anglais) vient de la contraction de « monade d'opérations » (operation monad en anglais). Ce terme a été utilisé pour la première fois par Peter May.

Voir aussi

• Algèbre sur un corps
• Catégorie
• Arbre

Références

• (en) Martin Markl, Steve Shnider, Jim Stasheff, Operads in Algebra, Topology and Physics, Providence, American Mathematical Society, 2002, poche (ISBN 978-0-8218-4362-8) (OCLC 48810307) (LCCN 2002016342) [lire en ligne] 

• (en) J. P. May, The Geometry of Iterated Loop Spaces, Berlin, Springer-Verlag, 1972, 1^re éd. (ISBN 978-3-540-05904-2) [lire en ligne] 

• J.-L. Loday, B. Vallette, Algebraic operads, preprint, 2010 [lire en ligne] 

• Jim Stasheff, « What Is…an Operad? », dans Notices of the American Mathematical Society, vol. 51, n^o 6, June/July 2004, p. 630–631 [texte intégral] 

• Portail des mathématiques