- Catégorie Groupoïde
-
Catégorie groupoïde
Pour les articles homonymes, voir Groupoïde.En mathématiques – plus particulièrement en théorie des catégories et en topologie algébrique – la notion de groupoïde généralise à la fois les notions de groupe, de relation d'équivalence sur un ensemble, et de l'action d'un groupe sur un ensemble. Elle a été initialement développée par le mathématicien Heinrich Brandt en 1927 [1]
Les groupoïdes sont souvent utilisés pour représenter certaines informations sur des objets topologiques ou géométriques comme les variétés.
Sommaire
Définition
Un groupoïde est une catégorie dans laquelle tout morphisme est un isomorphisme (c'est-à-dire est inversible).
Définition algébrique
Un groupoïde est un ensemble muni de deux opérations: une loi de composition partiellement définie * et une application (partout définie) −1, qui satisfont les trois conditions sur les éléments f, g et h de G:
- Chaque fois que f * g et g * h sont définis simultanément, alors (f * g) * h et f * (g * h) sont aussi définis, et sont égaux, on les note fgh ou f * g * h.
- f − 1 * f et f * f − 1 sont toujours définis (mais éventuellement différents).
- Chaque fois que f * g est défini, alors f * g * g − 1 = f, et f − 1 * f * g = g. (Ces expressions sont bien définies d'après les axiomes précédents).
On montre alors que
- (f − 1) − 1 = f
- Si x * f = u * f alors x = u
- Si f * y = f * v alors y = v
Les objets de la catégorie associée sont les x = f − 1 * f lorsque f varie (on remarque que ces éléments vérifient : x − 1 = x = xn). L'ensemble des morphismes x→y, noté G(f − 1 * f,g − 1 * g) = G(x,y), est l'ensemble des h tels que y * h * x est défini (cet ensemble pouvant être vide).
Exemples
- Les groupes sont des groupoïdes (avec un seul objet x et pour ensemble de flèches (morphismes) G(x,x) = G).
- Le groupoïde de poincaré est un groupoïde.
- En algèbre linéaire, le groupoïde GL * (K) des matrices carrées inversibles (de taille quelconque), l'ensemble des objets étant l'ensemble des entiers naturels, G(n,n)=GL(n,K), les matrices formant les morphismes.
- A partir d'une action de groupe on peut définir un groupoïde en posant G(x,y)=les éléments de G qui envoient x en y.
Propriétés
Les (petits) groupoïdes forment eux-mêmes une catégorie, les morphismes étant les foncteurs entre groupoïdes.
Soit G un groupoïde, on définit la relation d'équivalence
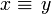si G(x,y) est non vide, elle définit un groupoïde quotient noté π0(G). π0 définit un foncteur (composantes connexes) de la catégorie des groupoïdes vers la catégorie des ensembles.Soit G un groupoïde, et x un objet de G (on dit aussi un point de G). La loi de composition entre les flèches de G(x,x) restreinte à ce sous-groupoïde est une loi de groupe. On note π1(G,x) ce groupe.
Notes et références
- ↑ Brandt H (1927) Über eine Verallgemeinerung des Gruppenbegriffes. Mathematische Annalen 96, 360-366.
Portail des mathématiques
Catégorie : Théorie des catégories
Wikimedia Foundation. 2010.
