- Carré logique
-
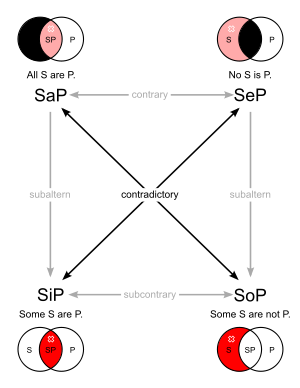
Le carré logique représente les oppositions logiques entre les différentes propositions :
- Proposition notée A, universelle affirmative : « tous les x sont P »
- Proposition notée E, universelle négative : « aucun x n'est P »
- Proposition notée I, particulière affirmative : « quelque x est P »
- Proposition notée O, particulière négative : « quelque x est non-P »
Deux propositions disposant des mêmes sujets et prédicat peuvent s'opposer par leur qualité et/ou par leur quantité. Ainsi les oppositions qui peuvent être créées sont les suivantes :
- Deux propositions contradictoires sont des propositions qui s'opposent par la qualité et la quantité
- Deux propositions contraires sont des propositions universelles qui s'opposent par la qualité
- Deux propositions subcontraires sont des propositions particulières qui s'opposent par la qualité
- Deux propositions subalternes sont des propositions qui s'opposent par la quantité
On établit ainsi le carré logique de l'opposition des propositions.
A : Tous les x sont P ←Contraire→ E : Aucun x n’est P ↕Subalterne↕ Contradictoire ↕Subalterne↕ I : Certain x est P ←Subcontraire→ O : Certain x est non-P Sommaire
Autres carrés
Créé au Moyen Âge[1], le carré logique présente une telle régularité que l'on a essayé, à l'époque moderne, de l'appliquer à plusieurs domaines formalisés :
- en sémiotique, le carré sémiotique a été développé par Greimas ;
- en logique modale, M. et W. Kneale[2] ont présenté le carré logique des modalités selon Diodore :
nécessaire (est vrai et ne sera pas faux) ←Contraire→ impossible (est faux et ne sera pas vrai) ↕Subalterne↕ Contradictoire ↕Subalterne↕ possible (est vrai ou sera vrai) ←Subcontraire→ non-nécessaire (est faux ou sera faux) - en logique épistémique, on a également pu se demander, à l'instar de Pascal Engel[3], si l'on peut concevoir un carré épistémique ;
- en sémantique argumentative, plus précisément, dans le cadre de la Théorie des blocs sémantiques[4], Marion Carel et Oswald Ducrot proposent un "carré argumentatif", inspiré du carré d'Aristote, reliant par des propriétés formelles des « prédicats argumentatifs » (dans leur terminologie, des "aspects argumentatifs") en « donc » et en "pourtant".
Références
- Roger Caratini, Introduction à la philosophie, L'Archipel (2000), p.407
- The Development of logic, Oxford, Clarendon Press, 1962, p. 125. Reproduit par Jules Vuillemin dans Nécessité ou contingence, Paris, Minuit, 1984, p. 78, note 33.
- « À quoi ressemblerait le carré logique épistémique ? », The Square of Opposition, International Congress, Montreux, 2 juin 2007.
- cf.Marion Carel et Oswald Ducrot (1999) « Le problème du paradoxe dans une sémantique argumentative », Langue française n°123 : 6-26. Marion Carel (2005) « La construction du sens des énoncés », Revue romane, n° 40-1, p. 79-97. Voir également Kohei Kida (1998) Une sémantique non véritative des énoncés conditionnels : essai de traitement argumentatif, thèse de doctorat (EHESS), p. 262-277.
Voir aussi
- Syllogisme
- Idéographie
- Carré sémiotique
- Logique : la théorie formelle des syllogismes, Marcel Crabbé
- Le carré logique et l'inférence immédiate
Liens externes
- Congrès mondial sur le carré des oppositions
- Numéro spécial de la revue Logica Universalis Vol2 N1 (2008) sur le carré des oppositions
Wikimedia Foundation. 2010.