Calculateur Mental

Le calcul mental est une pratique visant à effectuer des calculs sans l'aide d'aucun support autre que son imagination. Avant d'exposer les différentes techniques de calcul mental, il est essentiel de souligner que ces techniques ne sont pas naturelles et ne transforment pas quelqu'un qui ne sait pas compter en une calculatrice humaine en un clin d'œil ; il faut pour se les approprier s'entraîner, et les pratiquer régulièrement. La pratique de l'abaque, du boulier et plus précisément du boulier japonais, appelé soroban, permet d'augmenter les effets de manière spectaculaire par le biais de l'anzan.

Sommaire 1 Remarque préalable : mémorisation et conséquence sur la technique 2 Addition et soustraction 2.1 Remodeler les entiers pour la soustraction 2.2 Remodeler les entiers pour l'addition 2.3 Soustraction monétaire : combien dois-je rendre à mon client ? 3 Calcul d'un produit : ab × cd (théorie) 3.1 multiplier les unités 3.2 multiplier les dizaines 3.3 additionner les produits croisés 3.4 placer le résultat sous les produits précédents 3.5 tracer des lignes verticales 3.6 additionner les nombres entre les lignes 3.7 nous obtenons le résultat 4 Calcul d'un produit : 45 × 34 (exemple) 4.1 multiplier les unités 4.2 multiplier les dizaines 4.3 additionner les produits croisés 4.4 placer le résultat sous les produits précédents 4.5 tracer des lignes verticales 4.6 additionner les nombres entre les lignes 4.7 nous obtenons le résultat 5 Calcul d'un produit : a × b 5.1 Multiplier par 10 5.2 Multiplier par 2 5.3 Multiplication par 5 5.3.1 Diviser par 2 5.4 Multiplication par 9 5.5 Multiplication : {6 – 10} × {6 – 10} 5.6 Calcul du carré d'un entier ayant « 5 » comme chiffre des unités 5.7 Calcul du produit de deux entiers dans la même dizaine et dont les chiffres des unités se complètent 5.8 Multiplication d'un nombre par 11 5.8.1 Multiplication d'un nombre à deux chiffres par 11 5.8.2 Multiplication d'un nombre à trois chiffres par 11 5.9 Modulo 11 d'un nombre à 3 chiffres 5.10 Multiplication de deux nombres entiers compris entre 10 et 19 5.11 Méthode du train inverse 5.12 Utiliser les carrés 5.13 Remodeler les entiers 5.13.1 Multiplication croisée 5.14 Vérifier son résultat 5.14.1 Ordre de grandeur 5.14.2 Chiffre des unités 6 Calcul d'un quotient : a ÷ b 7 Calcul approximatif (Ordre de grandeur) 8 Calcul approché 9 Calcul approximatif d'une racine carrée 10 Calcul exact d'une racine carrée 11 Bibliographie 12 Articles connexes 13 Liens externes

Remarque préalable : mémorisation et conséquence sur la technique

Le calcul mental utilise

• la mémoire à long terme, sollicitée pour fournir un répertoire de résultats de calcul connus, l'exemple le plus typique étant une table de multiplication. Plus ce répertoire est étendu et moins il y a de calcul à faire.
• la mémoire à court terme, pour stocker les nombres sur lesquels on opère et les résultats intermédiaires. Cette mémoire n'est pas très étendue, elle permet de stocker une courte phrase et quelque nombres seulement, aussi faut-il réduire au minimum les retenues et autres résultats intermédiaire à stocker. De plus, elle est très volatile, on oublie en quelques secondes ce qu'on était en train de calculer, dès qu'on cesse de le faire. Aussi ne faut-il jamais s'arrêter en cours de calcul.

Un entrainement régulier permet d'augmenter la quantité de résultats déjà connus, et de renforcer la mémoire à court terme.

Addition et soustraction

L'addition est associative ( a + (b + c) = (a + b) + c ) et commutative ( a + b = b + a) : on peut donc associer et commuter les termes entre eux:

• 1 984 + 876 + 328 + 9 139 = (1000 + 900 + 80 + 4) + (700 + 100 + 70 + 6) + (300 + 20 + 8) + (9000 + 100 + 30 + 2 + 7)
• 1 984 + 876 + 328 + 9 139 = (1000 + 9000) + (900 + 100) + (700 + 300) + (80 + 20) + (70 + 30) + (4 + 6) + (2 + 8) + 100 + 7
• 1 984 + 876 + 328 + 9 139 = 10 000 + 1 000 + 1 000 + 100 + 100 + 100 + 10 + 10 + 7
• 1 984 + 876 + 328 + 9 139 = 12 327

Remodeler les entiers pour la soustraction

On transforme progressivement les nombres pour "arrondir" le nombre à soustraire et ainsi n'avoir plus que zéro à soustraire, en profitant du fait que

a – b = (a + c) – (b + c) = (a - d) – (b - d) .

Contrairement à l'algorithme usuel, on calcule de préférence des puissances élevées vers les unités (ce n'est pas obligatoire mais c'est plus commode pour la mémoire). Exemple :

1462 - 295

Lorsque le chiffre à soustraire, au cours d'une opération, est plus petit que le chiffre dont on doit le soustraire, on fait la soustraction directement :

1462 - 295 = (1462 - 200) - (295 - 200) = 1262 - 95

Lorsque le chiffre à soustraire est trop grand, on fait une addition, ce qui permet de matérialiser immédiatement la retenue sans avoir à la mémoriser en plus :

1262 - 95 = (1262 + 10) - (95 + 10) = 1272 - 105

Mais parfois il y a encore plus simple, car le but est d'arrondir progressivement le nombre à soustraire

1262 - 95 = (1262 + 5) - (95 + 5) = 1267 - 100

1267 - 100 = 1167

On peut ainsi, de manière générale, utiliser un complément à 10, 100, 1000 du soustracteur (car il est aisé de soustraire 10, 40, 100, 1000, par exemple) en ajoutant le même nombre à chacun des termes de la soustraction : 872 − 91 = 881 − 100 = 781 (on a ajouté 9). 8192 − 732 = 8160 − 700 = 7460 (on a enlevé 32).

Remodeler les entiers pour l'addition

Le principe reste le même, il s'agit d'arrondir et d'annuler progressivement la quantité à ajouter, mais cette fois il faut concevoir cela comme un déplacement de petits morceaux de la quantité à ajouter vers le nombre auquel on l'ajoute, ou parfois, pour éviter les retenues, dans l'autre sens.

a + (b + c) = (a + c) + b

ou

(a + c) + b = a + (b + c)

Là encore on calcule de préférence des puissances élevées vers les unités. Exemple :

1462 + 295 = 1462 + 200 + 95 = 1662 + 95

1662 + 95 = 1667 + 90 = 1757

Soustraction monétaire : combien dois-je rendre à mon client ?

Cette technique est très usuelle, on l'observe chez les commerçants qui rendent la monnaie.

On ramène la soustraction en une addition, à partir du nombre à soustraire (b), de la quantité suffisante pour obtenir le nombre dont on le soustrait (a). Le calcul est fait chiffre par chiffre et dans l'ordre usuel (des unités vers les dizaines, centaines, etc.) car, dans un contexte monétaire, il est possible de matérialiser immédiatement le résultat intermédiaire par une quantité de monnaie piochée dans la caisse, sans avoir besoin de le mémoriser.

Par exemple, 1462 - 295

• combien faut-il ajouter d'unité à 5 pour obtenir un 2 ? réponse 7, mais j'obtiens 12 et non 2 donc je retiens 1 ;
• combien faut-il ajouter de dizaines à 9 +1 (ma retenue), = 10 pour obtenir un 6 ? réponse 6, mais j'obtiens 16 et non 6 donc je retiens 1 ;
• combien faut-il ajouter de centaines à 2 +1 (ma seconde retenue), = 3 pour obtenir un 4  ? réponse 1
• combien faut-il ajouter de milliers à 0 pour obtenir 1 ? réponse 1
• c'est fini car j'ai atteint le total, la réponse est 1167

C'est encore plus facile si le nombre à atteindre est un chiffre rond commençant par un, comme c'est le cas lorsqu'il s'agit de rendre la monnaie : le chiffre à obtenir est le complémentaire à 10 de celui qui est à soustraire pour les unités et le complémentaire à 9 pour les autres, ce qu'on retient très vite avec un peu de pratique. Par exemple

10000 - 1062 = 9999 - 1062 + 1 (comme 9 est forcément supérieur ou égal à tous les chiffres rencontrés, il n'y a pas d'autre retenues que celle qui est appliquée d'entrée à l'unité)

unités : 10 - 2 = 8

dizaines : 9 - 6 = 3

centaines : 9 - 0 = 9

milliers : 9 - 1 = 8

résultat 8938

Calcul d'un produit : ab × cd (théorie)

multiplier les unités

   ab x cd = .....
    |    |
    b x  d = bd

multiplier les dizaines

   ab x cd = .....
   |    |
   a  x c  = ac

additionner les produits croisés

   ab x cd = .....
   ac   bd
   ad + bc = ef  

Attention à bien faire ad + bc et pas ac + bd ! ceci n'est vrai que dans le cas très particulier ou b=c (33, 22, 55 par exemple)

placer le résultat sous les produits précédents

   ab x cd = .....
    ac bd
     e f

tracer des lignes verticales

   ab x cd = .....
   a|c b|d
    |e f|

additionner les nombres entre les lignes

   ab x cd = .....
   a|c b|d
    |e f|
   -------
   a c b d
     + +
     e f

nous obtenons le résultat

   ab x cd = a ( c + e ) ( b + f ) d

Calcul d'un produit : 45 × 34 (exemple)

multiplier les unités

   45 x 34 = .....
    |    |
    5 x  4 = 20

multiplier les dizaines

   45 x 34 = .....
   |    |
   4  x 3  = 12

additionner les produits croisés

   45 x 34 = .....
   12   20

   4 5
   3 4 donne (on "croise" 4 avec 4 , 3 avec 5) : 4x4 + 5x3 = 16 + 15 = 31 

(on peut également "retourner" le nombre du haut : faire passer ab en ba, ici 45 en 54, et réitérer la méthode du début en n'oubliant pas d'additionner. C'est bien de axd + cxb dont il s'agit)

placer le résultat sous les produits précédents

   45 x 34 = .....
    12 20
     3 1

tracer des lignes verticales

   45 x 34 = .....
   1|2 2|0
    |3 1|

additionner les nombres entre les lignes

   45 x 34 = .....
   1|2 2|0
    |3 1|
   -------
   1 2 2 0 
     + +
     3 1

nous obtenons le résultat

   45 x 34 = .....
   1|2 1|5
    |3 1|
   -------
   1 2 2 0
     + +
     3 1
   -------
   1 5 3 0 

On prendra soin de vérifier à la calculatrice le résultat, au moins jusqu'à ce que la méthode soit acquise.

Calcul d'un produit : a × b

Multiplier par 10

Une multiplication par 10 consiste uniquement à rajouter un 0 à droite du nombre ; c'est donc une opération très élémentaire (s'il s'agit d'un nombre décimal, on décale la virgule d'une position vers la droite).

Multiplier par 2

C'est un cas particulier de multiplication, où l'on peut travailler chiffre à chiffre : si retenue il y a, c'est forcément 1, elle n'impacte que le dernier chiffre trouvé et il n'y a que peu de risque de retenu en cascade car cela voudrait dire qu'on est parti d'un nombre rempli de 9. On calcule de gauche à droite, en commençant par les chiffres représentant les puissances élevées, et en incorporant progressivement les retenues si elles apparaissent

2 × 16817 =

16817,

26817 (multiplication du 1, pas de retenue, je pose 2)

32817 (multiplication du 6, =12, une retenue : le 2 devient 3, je pose le 2 de 12 ce qui donne 32)

33617 (multiplication du 8, =16, une retenue : le 32 devient 33, je pose le 6 de 16 ce qui donne 336)

33627 (multiplication du 1,=2 pas de retenue, 3362)

33634 multiplication du 7, =14, une retenue : le 3362 devient 3363, je pose le 4 de 14, c'est fini)

Multiplication par 5

Il s'agit d'une multiplication par 10 suivie d'une division par 2 ; donc pour multiplier par 5, il suffit de savoir diviser par 2.

Diviser par 2

Il faut lire le nombre de gauche à droite, et diviser les chiffres par 2 arrondi à l'entier inférieur puis ajouter 5 au résultat de la division par 2 du chiffre suivant si le chiffre qu'on a divisé était impair. Par exemple

176 × 5 = 1760 ÷ 2,

1 divisé par 2 = 0 mais comme 1 est impair on ajoute 5 au résultat suivant

7 divisé par 2 = 3.5 on garde 3 et on ajoute 5 de l'opération précédente donc 3+5 = 8

6 divisé par 2 = 3 et on ajoute 5 de l'opération précédente car 7 est impair donc 3+5 = 8

0 divisé par 2 = 0

le résultat est 0880 soit 176x5 = 880

Multiplication par 9

Il suffit de remarquer que 9 = 10 – 1, donc pour multiplier par 9, il suffit de multiplier le nombre par 10, et de le soustraire au résultat ; par exemple, 9 × 27 = 270 – 27 = 243. Il faut donc savoir soustraire…

Autre technique : avec les doigts de la main. On place ses deux mains face à soi et on replie le doigt que l'on veut multiplier par 9.

exemple : 9 x 4; on replie le 4^e doigt en partant de gauche. il reste 3 doigts à gauche et 6 à droite

9 x 4 = 36

9 x 7 ; on plie le 7^e doigt et on a 6 et 3

9 x 7 = 63

Multiplication : {6 – 10} × {6 – 10}

Cette technique permet de multiplier un nombre entre 6 et 10 par un autre entre 6 et 10.

Cette technique utilise les dix doigts des deux mains, face à face :

-10-- -10--
--9-- --9--
--8-- --8--
--7-- --7--
--6-- --6--

Deux exemples :

• 9 × 6

haut :
      -10--
      --9--
      --8--
-10-- --7--
bas :
--9-- --6--
--8-- 
--7-- 
--6--  

Les dizaines (on compte les doigts du bas, soit 4 + 1 = 5 dizaines) :

--9-- --6--
--8-- 
--7-- 
--6--  

Les unités (on multiplie le nombre de doigts en haut à gauche par ceux en haut à droite, soit 1 x 4 = 4 unités) :

      -10--
      --9--
      --8--
-10-- --7--

résultat : 9 × 6 = 50 + 1 x 4 = 54

• 6 × 8

haut :
-10--
--9-- 
--8-- -10--
--7-- --9--
bas :
--6-- --8--
      --7--
      --6--

Les dizaines (on compte les doigts du bas, soit 1 + 3 = 4 dizaines) :

--6-- --8--
      --7--
      --6--

Les unités (on multiplie le nombre de doigts du haut à gauche par ceux en haut à droite, 4 x 2 = 8 unités) :

-10--
--9-- 
--8-- -10--
--7-- --9--

résultat : 6 × 8 = 40 + 4 x 2 = 48

• X × Y

-10-- -10--
--9-- --9--
--8-- --8--
--7-- --7--
--6-- --6--

Le fonctionnement : chaque doigt représente un chiffre (entre 6 et 10). On joint les deux doigts dont on veut multiplier les chiffres correspondants (x et y). Les doigts en bas indiquent les dizaines, on en a (x – 5) + (y – 5). Les doigts à gauche en haut indiquent (10 – x) et ceux à droite en haut (10 – x).

Et :
  [(x – 5) + (y – 5)] × 10 + (10 – x) × (10 – y)
= (x + y - 10) × 10 + (100 - 10y - 10x + x × y) 
= 10x + 10y - 100 + 100 - 10y - 10x + x × y
= x × y

Calcul du carré d'un entier ayant « 5 » comme chiffre des unités

Pour calculer un tel carré, il suffit de calculer le produit du nombre qu'on forme en effaçant ce chiffre « 5 » par le nombre entier suivant et de faire suivre l'écriture obtenue des deux chiffres « 25 ». Par exemple pour calculer 85², on calcule le produit 8 × 9 = 72 et on trouve ainsi que 85² = 7 225.

Calcul du produit de deux entiers dans la même dizaine et dont les chiffres des unités se complètent

Commencer par multiplier les deux chiffres des unités entre eux puis faire précéder l'écriture obtenue, au niveau des centaines, par l'écriture du produit de ce nombre commun de dizaines par le nombre entier suivant.

Exemples :

• Pour calculer 57 × 53, on calcule 7 × 3 = 21 et 5 × 6 = 30. On trouve alors 57 × 53 = 3 021.
• Pour calculer 71 × 79, on calcule 1 × 9 = 9 et 7 × 8 = 56. On trouve alors 71 × 79 = 5 609.

Cette technique est une généralisation de la technique Calcul du carré d'un entier ayant « 5 » comme chiffre des unités. Sa validité provient du calcul suivant, où a désigne le nombre entier commun de dizaines et b l'une des deux unités complémentaires :

(10a + b)(10a + (10 − b)) = 100a² + 10a(b + 10 − b) + b(10 − b) = 100a(a + 1) + b(10 − b)

Multiplication d'un nombre par 11

Multiplication d'un nombre à deux chiffres par 11

Une astuce consiste à faire la somme du premier chiffre avec le second, puis de l'ajouter entre les deux

Si la somme est inférieure à 10.

Exemples :

17 × 11 = 1 (1+7) 7 = 187

35 × 11 = 3 (3+5) 5 = 385

Si la somme est supérieure à 10, on place le chiffre des unités de la somme entre les deux chiffres et on ajoute 1 aux centaines.

Exemples :

58 × 11 = 5 (5+8) 8 = 5 (13) 8 = (5+1) 3 8 = 638

93 × 11 = 9 (9+3) 3 = 9 (12) 3 = (9+1) 2 3 = 1023

Multiplication d'un nombre à trois chiffres par 11

La technique est à peu près la même que pour les nombres à deux chiffres.

1. On garde le premier chiffre,
2. On ajoute juste après la somme des 2 premiers chiffres qui doit être inférieure à 10,
3. On ajoute la somme des 2 derniers chiffres qui doit être inférieure à 10,
4. On ajoute enfin le dernier chiffre.

Ainsi on a 123 x 11 = 1353, avec le premier chiffre 1, suivi de 3 (1+2 =3), puis 5 (2+3=5), puis le dernier chiffre 3.

Deuxième technique avec toujours le nombre 123:

1)On conserve toujours le premier chiffre et le dernier chiffre (c'est à dire le 1 et le 3) du nombre 123 qui maintiendrons leur place initiale pour le résultat final.

2)On garde les deux premiers chiffres (12)du nombre 123 et les deux derniers chiffres (23) du nombre 123 pour les additionner: 12+23=35

3)Résultat final donne le 1 3 et on ajoute au milieu la somme qu'on a trouvé ci dessus(35)cela donne 1353 donc 123 x 11 = 1353

Remarque cet exemple n'est pas trop différent du premier mais ceux qui préfèrent additionner en vertical qu'en horizontal(linéaire) seront ravis. Mais il faut être à l'aise avec les additions à deux chiffres.

Si une des deux additions donne un résultat supérieur à 10, il est plus facile de commencer à l'envers :

1. On garde le dernier chiffre,
2. On ajoute juste avant la somme des 2 derniers chiffres,
3. On ajoute aussi avant la somme des 2 premiers chiffres incrémentée de 1 si l'opération 2 a donné un résultat supérieur à 10.
4. On ajoute enfin le premier chiffre incrémenté de 1 si l'opération 3 a donné un résultat supérieur à 10.

Modulo 11 d'un nombre à 3 chiffres

Voici une technique pour calculer le modulo 11 d'un nombre à trois chiffres:

1. On additionne le premier et le dernier chiffre,
2. On soustrait le chiffre central du résultat de l'opération précédente,
3. Si le résultat de la soustraction est positif, on a le modulo, s'il est négatif, on lui ajoute 11 pour avoir le modulo.

Exemples:

• 652 modulo 11: 6 + 2 - 5 = 3
• 183 module 11: 1 + 3 - 8 = -4, -4 + 11 = 7

Multiplication de deux nombres entiers compris entre 10 et 19

Pour multiplier les deux nombres, la technique est la suivante :

1. on additionne le premier nombre et les unités du deuxième nombre puis on ajoute un zéro (on multiplie par 10)
2. on additionne au nombre obtenu le produit des unités des deux nombres

Exemple avec 17 × 18 :

1. 17 + 8 = 25 , on ajoute 0, ce qui donne 250
2. 7 × 8 = 56 et 250 + 56 = 306, donc 17 × 18 = 306

Exemple avec 14 × 17 :

1. 14 + 7 = 21, on ajoute 0, ce qui donne 210
2. 4 × 7 = 28 et 210 + 28 = 238, donc 14 × 17 = 238

Démonstration :

• soient A et B deux nombres entre 10 et 19
• on note a et b deux chiffres (entre 0 et 9) tel que A = 10 + a et B = 10 + b
• on cherche le résultat de A×B, qui s'écrit également (10 + a)×(10 + b)
• en développant, on obtient : 10×10 + 10×a + 10×b + a×b
• en regroupant un peu, on obtient 10×(10 + a + b) + a×b
• donc 10×(A + b) + a×b

Méthode du train inverse

Soit à multiplier, par exemple, 709801 (multiplicande) par 58 (multiplicateur).

L'étape préliminaire est d'écrire le multiplicateur dans l'ordre inverse, 58 devient 85. 
La méthode consiste ensuite de faire glisser le multiplicateur retourné le long des chiffres du multiplicande, 
comme un train longeant un quai, puis de faire la somme des produits.

Étape 1 
   709801
  85       on calcule 5x7 = 35,        on conserve : 35  <-- ligne d'ordre 'zéro'

Étape 2
   709801
   85      on calcule 8x7 + 5x0 = 56,  on conserve : 356
                                                      5  <-- ligne d'ordre 'un' (retenues des dizaines - 56 est écrit en diagonal)
Étape 3
   709801
    85     on calcule 8x0 + 5x9 = 45,  on conserve : 3565
                                                      54  
Étape 4
   709801
     85    on calcule 8x9 + 5x8 = 112, on conserve : 35652
                                                      541  
                                                       1   <-- ligne d'ordre 'deux' (retenues des centaines - 112 est écrit en diagonal)
Étape 5
   709801
      85   on calcule 8x8 + 5x0 = 64,  on conserve : 356524
                                                      5416  
                                                       1   
Étape 6
   709801
       85  on calcule 8x0 + 5x1 = 5,   on conserve : 3565245
                                                      5416  
                                                       1   
Étape 7
   709801
        85 on calcule 8x1 = 8,         on conserve : 35652458
                                                      5416  
                                                       1   
Dernière étape : on additionne les lignes des retenues ce qui donne :
   35652458
  + 5416  
  +  1   
  =41168458

Remarque : un certain nombre de méthodes particulière de calcul mental s'explique par cette méthode générale (qui n'est qu'une autre façon de poser la multiplication). Par exemple la multiplication par '11' : on remarque immédiatement que la multiplication par '11' s'effectue en conservant le premier et le dernier chiffres et les chiffres intermédiaires sont la somme de deux chiffres successifs.

Utiliser les carrés

On peut utiliser les carrés des entiers, pour calculer des produits pour les petits nombres ; par exemple, pour calculer 13 × 17, on peut remarquer que l'on est en train de calculer (15 – 2) × (15 + 2), donc 15² – 2², d'après l'une des identités remarquables, c'est-à-dire 225 – 4 = 221, ce qui donne le résultat très rapidement, puisque l'opération devient une simple soustraction.

Cela demande néanmoins de connaître par cœur un certain nombre de carrés :

• 1² = 1
• 2² = 4
• 3² = 9
• 4² = 16
• 5² = 25
• 6² = 36
• 7² = 49
• 8² = 64
• 9² = 81
• 10² = 100
• 11² = 121
• 12² = 144
• 13² = 169
• 14² = 196
• 15² = 225
• 16² = 256
• 17² = 289
• 18² = 324
• 19² = 361

Il faut néanmoins remarquer que si on ne connaît que certains de ces carrés, les identités remarquables permettent de calculer les autres facilement…

Remodeler les entiers

Le calcul à effectuer ne fait pas forcément intervenir des nombres qui se prêtent aux techniques précédentes, néanmoins, on peut forcer le passage de diverses manières :

• décaler le problème : pour calculer 13 × 18, on regrette de ne pas avoir à calculer 13 × 17, où l'on dispose de la technique des carrés : il suffit de voir 13 × 18 comme 13 × 17 + 13, et on a : 225 – 4 + 13 = 234 ;
• factoriser version 1 : pour calculer 27 × 72, il suffit de se débarrasser des multiplications par 2 (faciles) qui sont cachées derrière : 72 = 2 × 36 = 2 × 2 × 2 × 9, donc il suffit de calculer 27 × 9 puis multiplier par 2 trois fois de suite :

27 × 9 = 243, puis 243 × 2 = 486, 486 × 2 = 972, et finalement 972 × 2 = 1944.

• factoriser version 2 : pour calculer 13 × 18, on factorise une fois et on obtient 10 × 18 + 3 × 18 puis on recommence pour chaque multiplication

10 × 18 = 10 × 10 + 10 × 8 = 100 + 80 = 180 et 3 × 18 = 3 × 10 + 3 × 8 = 30 + 24 = 54 ; au final on a 180 + 54 = 234 (cette technique nécessite uniquement d'avoir de la mémoire et marche pour n'importe quel type de multiplication).

Multiplication croisée

Cette technique est très répandue dans les compétitions de calcul mental. En voici un exemple d'utilisation :

Soit à multiplier 8397 par 5621. On écrit les deux nombres l'un au-dessus de l'autre.

La première colonne montre un schéma correspondant à l'étape de calcul. La seconde colonne montre le calcul correspondant. La troisième colonne indique le nombre posé (écrit) et la quatrième colonne montre la retenue.

Schéma	Calcul	Posé	Retenu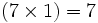
		7	0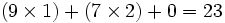
		3	2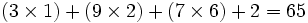
		5	6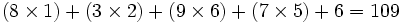
		9	10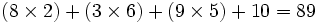
		9	8
		1	7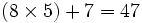
		7	4

Remarque : dans les étapes de calcul, la retenue peut parfois être supérieure à 9.

On écrit la dernière retenue puis tous les résultats posés dans l'ordre inverse de celui où ils ont été calculés : soit : 4, 7, 1, 9, 9, 5, 3, 7. .

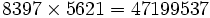Vérifier son résultat

Ordre de grandeur

Si en multipliant deux nombres plus petits que 100 on trouve plus de 10 000, il y a assurément un problème ! Ces considérations sont très empiriques et ne repèrent que les erreurs grossières, mais c'est la méthode la plus rapide. Ainsi la relativité, art complexe s'il en est, est là pour nous raisonner.

Chiffre des unités

Si vous multipliez les chiffres des unités de a et b, le chiffre des unités du résultat est le chiffre des unités de a × b ; exemple : 27 × 72 doit finir par un 4. Cette vérification permet de vérifier un chiffre avec certitude.

Calcul d'un quotient : a ÷ b

Pour calculer un quotient, on peut diviser le dividende et le diviseur par le même nombre :

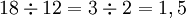• (on a simplifié par 6)
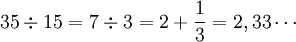• (on a simplifié par 5)

Calcul approximatif (Ordre de grandeur)

Commencer les produits par la partie gauche et simplifier : 117 × 34 = ?

• 100 × 30 + r₁ = 3000 + r₁ (négliger le reste r₁)
• un peu mieux
  • 100 × 30 + 20 × 30 + r₂ = 3000 + 600 + r₂ = 3600 + r₂
  • 100 × 30 + r₁ = 3600 + r₂
• encore mieux
  • 120 × 34 + r₃ = 100 × 30 + 20 × 30 + 120 × 4 + r₃ = 3000 + 600 + 480 + r₃ = 4080 + r₃
• Finalement
  • 117 × 34 = 100 × 30 + 20 × 30 + 120 × 4 – 3 × 30 – 3 × 4
  • 117 × 34 = 3000 + 600 + 480 - 90 - 12
  • 117 × 34 = 3978 (simple)
• Les restes se précisent au fur et à mesure : |r₁| > |r₂| > |r₃|. Où |x| est la valeur absolue de x, c'est-à-dire x en valeur positive.
• D'où 117 × 34 est :
  • en première évaluation proche de 3000
  • en deuxième évaluation proche de 3600
  • en troisième évaluation proche de 4080
  • en quatrième évaluation proche de 3990
  • finalement égal à 3978

Toutes les méthodes exposées dans l'article peuvent se combiner.

117 × 34 ≠ 120 × 35 = 120 × 70 ÷ 2 = 60 × 70 = 4200

117 × 34 ≠ 120 × (100 ÷ 3) = 4000

Calcul approché

La connaissance du développement limité d'une fonction au voisinage d'un point (0 en particulier) permet de calculer des valeurs approchées.

Exemple

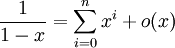donc 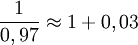car 0,97 = 1 − 0,03, en considérant que 0,03 est proche de zéro. On peut affiner le calcul : 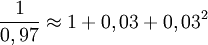, soit 1,0309.

Calcul approximatif d'une racine carrée

Cette technique permet d'obtenir environ trois bonnes décimales par opération. On doit savoir que (a – b)² = a² – 2ab + b² Il suffit de choisir un b tellement petit que le terme b² est négligeable. Par exemple, si on a la racine de 15 à calculer, on sait que la racine de 16 est 4. On doit prendre un b qui fait que (4 – b)² = 15 ou presque. Puisque (4 – b)² = 16 – 2 × 4 × b environ, on prend b = (16 – 15) ÷ (2 × 4), c'est-à-dire 1/8 ou 0,125. La racine carrée de 15 vaut donc environ 4 – 0,125 ou 3,875. Si on veut plus de précision, on recommence. Puisque notre 4 initial était à notre choix, on peut recommencer avec 3,88 au lieu, si on trouve que 3,875 est trop précis. Nous avons donc (3,88 – b)² = 15. b = (3,88² - 15) ÷ (2 × 3,88) = (15,054 – 15) ÷ (7,76) = environ 0,054 ÷ 8 donc environ 0,00675. La racine de 15 est maintenant évaluée à 3,88 – 0,00675 ou 3,87325. La valeur donnée par une calculatrice est 3,8730.

Calcul exact d'une racine carrée

Cette technique permet d'obtenir autant de décimales que nécessaire, en combinant additions et soustractions. Le procédé est itératif et présente l'avantage de fournir un chiffre exact de la racine à chaque itération.

Explication (et exemple avec le calcul de la racine de 5337) :

• séparer le nombre dont on extrait la racine, en groupes de 2 chiffres en partant de la virgule (5337 donne 53 | 37 , 00 …) ;
• prendre la tranche la plus à gauche et lui soustraire successivement tous les entiers impairs consécutifs, tant que le résultat obtenu est positif (ici : 53 -1-3-5-7-9-11-13 = 4) ;
• le nombre de soustractions effectuées fournit le premier chiffre de la racine (ici 7) ;
• accoler au résultat partiel des précédentes soustractions, le groupement de chiffres suivant (ici 4 et 37 => 437) ;
• lui soustraire successivement tous les entiers impairs consécutifs, en partant du dernier nombre soustrait, incrémenté et accolé de 1, tant que le résultat obtenu est positif (437 - ((13 + 1)1 => 141) - 143 - 145 = 8) ;
• le nombre de soustractions effectuées fournit le second chiffre de la racine (3) ;
• réitérer le processus afin d'augmenter la précision du résultat obtenu… (800 - ((145+1)1 => 1461) négatif).
• Attention, au cas où il n'est pas possible d'effectuer la moindre soustraction sans obtenir un résultat négatif, pour pouvoir continuer le procédé, il faut accoler le groupe de chiffres suivant, mais, pour obtenir les nombres à soustraire, il faut remplacer le dernier 1 par 0 et accoler ensuite un autre 1. (80 000 - ((1461-1)1 => 14 601) - 14 603 - 14 605 - 14 607 - 14 609 = 6975).

Ainsi en première approximation, il est possible de trouver que la racine de 5337 est 73,05.

Bibliographie

• René Taton, Le calcul mental (1953), Presses universitaires de France, coll. Que sais-je ?
• Émile Fourrey, Récréations arithmétiques (1933), éd. Vuibert

Articles connexes

• Méthode Trachtenberg
• S'initier au boulier en 10 leçons : Une fois assimilée la technique manuelle du calcul sur boulier, on peut visualiser un boulier, et faire les calculs de tête
• Calculateur prodige
• Calcul Mental
• Anzan

Liens externes

• TuXmath, un petit jeu (libre) de calcul mental

• Fédération française de soroban et autres abaques
• Fédération française de calcul mental
• Association française de soroban et autres abaques
• Association française de calcul mental
• Tournoi de Calcul Mental : concours scolaire et concours tout public