- Modèle booléen
-
Un modèle booléen est une méthode ensembliste de représentation du contenu d'un document. C'est l'un des premiers modèles utilisés en recherche d'information, permettant de fouiller automatiquement les grand corpus de bibliothèques. Il en existe un modèle étendu qui généralise également le modèle vectoriel.
Sommaire
Modèle standard
Le modèle booléen est une représentation mathématique du contenu d'un document, selon une approche ensembliste.
Les documents sont représentés par des ensembles de termes et les requêtes traitées comme des expressions logiques. Considérant un vocabulaire
 , un document est caractérisé par la présence ou l'absence de chaque ti dans son contenu. La requête s'exprime alors avec des opérateurs logiques selon le formalisme de l'algèbre de Boole. Un document du corpus est ainsi considéré comme pertinent uniquement quand son contenu est vrai pour l'expression de la requête.
, un document est caractérisé par la présence ou l'absence de chaque ti dans son contenu. La requête s'exprime alors avec des opérateurs logiques selon le formalisme de l'algèbre de Boole. Un document du corpus est ainsi considéré comme pertinent uniquement quand son contenu est vrai pour l'expression de la requête.Avantages et inconvénients
La simplicité du modèle le rend aisément compréhensible pour un utilisateur. Dans le cas de corpus explorés par des spécialistes, ayant notamment une très bonne connaissance du vocabulaire, cela le rend très efficace.
Cette simplicité le rend néanmoins peu adapté à des recherches sur des corpus généralistes, surtout lorsque les utilisateurs n'ont pas d'expertise sur ce dernier. En particulier, la formulation des requêtes devient vite laborieuse quand la requête se fait précise (donc longue). Un autre inconvénient majeur du modèle dans sa version la plus simple est l'impossibilité de rendre compte d'une correspondance partielle d'un document à une requête. Enfin, la pondération binaire des termes du vocabulaire limite la pertinence des résultats et ne permet pas de les ordonner.
Une part des inconvénients du modèle booléen standard est corrigé avec l'utilisation du modèle vectoriel ou du modèle booléen étendu.
Modèle étendu
L'extension du modèle booléen standard généralise également le modèle vectoriel. Il consiste principalement à pondérer les termes des documents au moyen d'un schéma tel celui du TF-IDF. Elle a été proposée par Salton, Fox et Wu en 1983[1]
Si on munit l'espace (vectoriel) de représentation d'une métrique Lp, un document peut ainsi appartenir à l'intérieur de la boule ouverte définie par l'intersection de la boule unité et de
 (autrement dit « entre 0 et 1 pour chaque dimension »), alors que le modèle booléen standard le contraint à appartenir à l'adhérence de celle-ci (i.e ses coordonnées ne peuvent que 0 ou 1).
(autrement dit « entre 0 et 1 pour chaque dimension »), alors que le modèle booléen standard le contraint à appartenir à l'adhérence de celle-ci (i.e ses coordonnées ne peuvent que 0 ou 1).Dans le cas d'une requête comportant deux termes, une condition logique de type ET est alors représentée par la distance entre le document est les coordonnées « idéales » (1,1) tandis qu'une condition de type OU est calculée par la distance du document à l'origine. Cette définition peut être généralisée à un nombre quelconque de termes.
Formulation pour deux termes
Considérons le cas d'un requête ne comportant que deux termes T1 et T2 et examinons le cas des requêtes disjonctives (T1 ET T2) et conjonctives (T1 OU T2), le but étant d'ordonner les documents Dj en réponse à cette requête q.
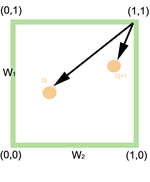
Dans le cas d'une requête
 (i.e T1 ET T2), le point idéal est (1,1) représentant le cas où les deux termes sont présents dans le document. Ainsi, la similarité de la requête q à un document est donnée par:
(i.e T1 ET T2), le point idéal est (1,1) représentant le cas où les deux termes sont présents dans le document. Ainsi, la similarité de la requête q à un document est donnée par:Dans le cas de la requête
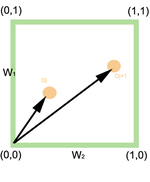
 (i.e T1 OU T2) il s'agit d'être le plus éloigné possible de l'origine (0,0) qui représente le pire cas où aucun des deux termes n'est présent. Ainsi:
(i.e T1 OU T2) il s'agit d'être le plus éloigné possible de l'origine (0,0) qui représente le pire cas où aucun des deux termes n'est présent. Ainsi:Généralisation à un nombre quelconque de termes
Les requêtes conjonctives et disjonctives peuvent être généralisées aux cas où la requête comporte plus de deux termes (m termes). On utilise pour cela les p-normes qui dépendent d'une paramètre p pouvant varier dans l'ensemble des entiers naturels. La généralisation de la similarité conjonctive (OU) s'exprime ainsi:
Et la généralisation d'une requête disjonctive (ET) par:
Quand le paramètre p=1 on retrouve le cas du modèle vectoriel tandis que lorsque p tend vers l'infini, on se ramène au cas du modèle booléen standard, avec des requêtes ET et OU strictes. En ce sens, le modèle booléen étendu est une généralisation de ces deux modèles.
Combinaison de requêtes conjonctives et disjonctives
La généralisation précédente s'applique à des requêtes conjonctives ou disjonctives « pures », c'est-à-dire ne comportant que l'un des opérateur ET ou OU à l'exclusion de l'autre. Le modèle booléen étendu permet néanmoins de les combiner les opérateurs[2] au moyen de regroupements récursifs.
Par exemple, pour la requête
 , la similarité entre la requête q et un document D comportant les trois termes pourra s'exprimer par:
, la similarité entre la requête q et un document D comportant les trois termes pourra s'exprimer par:Voir aussi
Liens externes
Références
- Gerard Salton,Edward A. Fox, Harry Wu, Extended Boolean information retrieval, Communications of the ACM,Volume 26 , Issue 11 ,1983
- R. Baeza-Yates, B. Ribeiro-Neto; Modern Information Retrieval Chapter 2, p. 40; Addison-Wesley (1999)
Wikimedia Foundation. 2010.

 ) entre une requête
) entre une requête 
 entre une requête
entre une requête 
![sim(q_{or},D_j)=\sqrt[p]{\frac{w_1^p+w_2^p+....+w_m^p}{m}}](3/d43385f3f4768b7a1ce16324cb1a9e28.png)
![sim(q_{and},D_j)=1-\sqrt[p]{\frac{(1-w_1)^p+(1-w_2)^p+....+(1-w_m)^p}{m}}](b/68bfa849a0107d3f46132cf729b892ef.png)
![sim(q,D)=\sqrt[p]{\frac{\left( 1-\sqrt[p]{(\frac{(1-w_1)^p+(1-w_2)^p}{2}})\right)^p + w_3^p}{2}}](b/20b7fa17d96687c8befc0dcc02cb6f93.png)