- Lemme de Sperner
-
En mathématiques, le lemme de Sperner, dû à Emanuel Sperner[1], est un analogue combinatoire du théorème du point fixe de Brouwer. Le lemme de Sperner affirme que chaque coloriage de Sperner d'une triangulation d'un simplexe de dimension n contient une cellule colorée de toutes les n+1 couleurs. Le premier résultat de ce type fut démontré par Emanuel Sperner en 1928, en relation avec des preuves du théorème de l'invariance du domaine. Les coloriages de Sperner ont été utilisés pour des déterminations effectives de points fixes, dans des algorithmes de résolution d'équations, et sont employés dans des procédures de partage équitable.
Sommaire
En dimension 1
En dimension 1, le lemme de Sperner peut être vu comme une version discrète du théorème des valeurs intermédiaires. Il affirme essentiellement qu'une fonction définie en un nombre fini de points, ne prenant que les valeurs 0 et 1, commençant à la valeur 0 et terminant en 1, doit changer de valeur un nombre impair de fois. Sur la figure de droite, ceci est représenté par les deux couleurs, avec 5 changements de couleurs de haut en bas.
En dimension 2
Le lemme de Sperner pour les triangles (les triangles dont il affirme l'existence (en nombre impair) sont colorés en gris)Le cas de la dimension 2 est celui auquel on se réfère le plus souvent. Il s'énonce ainsi :
On se donne un triangle ABC, et une triangulation T de ce triangle. L'ensemble S des sommets de T est coloré avec 3 couleurs, de telle sorte que
- A, B et C sont colorés respectivement des couleurs 1, 2 et 3.
- Les sommets situés sur un côté de ABC sont coloriés avec l'une des deux couleurs des extrémités de ce côté. Par exemple, chaque sommet sur AC doit recevoir la couleur 1 ou 3.
Il existe alors un triangle de T, dont les sommets sont colorés avec les trois couleurs. Plus généralement, il y a un nombre impair de tels triangles.
Cas général
Dans le cas général, le lemme concerne un simplexe de dimension n
Soit T une triangulation, c'est-à-dire une partition de
en simplexes de dimension n, plus petits et disjoints. Soit une fonction de coloriage f : S → {1,2,3,...,n,n+1}, où S est l'ensemble des sommets de T, respectant les règles de coloriage suivantes :- Les sommets du grand simplexe sont colorés de couleurs distinctes, et plus précisément f(Ai) = i pour 1 ≤ i ≤ n+1.
- Les sommets de T situés sur une sous-face de dimension k
- sont coloriés uniquement avec les couleurs
Il existe alors un nombre impair de simplexes de T, dont les sommets sont colorés avec les n+1 couleurs ; en particulier, il en existe au moins un.
Démonstration
Considérons d'abord le cas de la dimension 2. Soit G le graphe (non orienté) construit à partir de la triangulation T de la manière suivante :
- Les sommets de G sont les régions de T et la région à l'extérieur du triangle. Deux sommets sont reliés si les régions correspondantes ont une frontière commune, dont un des sommets est coloré 1 et l'autre 2.
Sur l'intervalle AB, il y a un nombre impair de segments colorés 1-2 (puisque A est coloré 1 et B est coloré 2, en allant de A à B, on doit rencontrer un nombre impair de changements de couleur). Ainsi, le sommet de G correspondant à l'extérieur du triangle est de degré impair. Dans un graphe fini, le nombre des sommets de degré impair est pair (lemme des poignées de main (en)), aussi il y a un nombre impair de sommets correspondants aux triangles de T, et ayant un degré impair. Or on voit facilement que les seuls degrés possibles de ces triangles sont 0, 1 ou 2, et que le degré 1 correspond aux triangles colorés avec les 3 couleurs 1, 2 et 3.
Le cas général (de dimension n) se démontre alors par récurrence sur n, en appliquant le même argument : deux sommets du graphe G sont reliés si les régions correspondantes ont une face commune (de dimension n-1), dont les sommets sont tous de couleurs différentes.
Généralisations
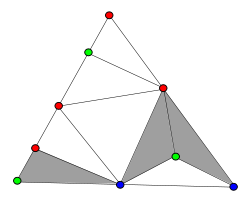
Le lemme de Sperner a été généralisé au coloriage d'un polytope triangulé ayant n sommets. Dans ce cas, il y a au moins n-k simplexes complètement coloriés, où k est la dimension du polytope et "complètement colorié" signifie que chacun des sommets du simplexe a une couleur différente. Par exemple, si un polygone à n sommets est triangulé et colorié en respectant la règle de Sperner, il y aura au moins n-2 triangles dont les trois sommets auront une coloration différente. Le résultat général fut conjecturé par Krassimir Atanassov (en) en 1996, qui le démontra[2] pour le cas k=2. Une démonstration du cas général fut obtenue par de Loera, Peterson, et Su en 2002[3].
Applications
Les coloriages de Sperner sont utilisés pour la détermination effective de points fixes : on associe à une fonction donnée f un coloriage de Sperner, et en choisissant des triangulations de plus en plus fines, on montre que les simplexes complètement colorés convergent vers un point fixe de f (c'est en particulier ainsi qu'on démontre le théorème du point fixe de Brouwer). Comme la détermination d'un simplexe complètement coloré est non seulement effective, mais qu'on dispose d'algorithmes rapides pour le faire, cette technique donne un procédé pratique pour obtenir des valeurs approchées des points fixes.
Pour la même raison, ces coloriages s'appliquent à la résolution d'équations, et on a pu également les utiliser pour la construction de procédures de partage équitable[4].
Voir aussi
Notes et références
- Selon la Mathematical Encyclopaedia soviétique (éditée par Ivan Vinogradov), un théorème voisin, obtenu en 1929 par Knaster (en), Borsuk etMazurkiewicz, était aussi connu comme lemme de Sperner. Il est à présent plus souvent mentionné comme le lemme de Knaster–Kuratowski–Mazurkiewicz.
- K. T. Atanassov, « On Sperner's Lemma », dans Stud. Sci. Math. Hungarica, vol. 32, 1996, p. 71–74
- Jesus de Loera, Elisha Peterson, et Francis Su, « A polytopal generalization of Sperner's Lemma », dans Journal of Combinatorial Theory Series A, vol. 100, 2002, p. 1–26 [lien DOI]
- Francis Edward Su, Rental Harmony: Sperner's Lemma in Fair Division Amer. Math. Monthly, 106(1999), 930-942.http://www.math.hmc.edu/~su/papers.dir/rent.pdf
Liens externes
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sperner's lemma » (voir la liste des auteurs)
Catégories :- Analyse combinatoire
- Topologie
- Théorème de la théorie des graphes
- Lemme de mathématiques
Wikimedia Foundation. 2010.
