Condition d'extinction

En cristallographie, les conditions d'extinction donnent l'ensemble des réflexions systématiquement absentes, c'est-à-dire d'intensité nulle, lors d'expériences de diffraction (de rayons X, de neutrons ou d'électrons) sur un cristal. Ces extinctions sont dues aux interférences destructives des rayons diffractés, causées par la présence d'opérations de symétrie contenant des composantes translatoires dans le groupe d'espace du cristal. Les réflexions systématiquement éteintes par symétrie sont appelées « réflexions interdites ». Les conditions de réflexion donnent, au contraire, pour un groupe d'espace donné, l'ensemble des réflexions d'intensité non nulle ou « réflexions autorisées » (même si dans la pratique certaines intensités mesurées peuvent être très faibles).

Il existe trois types d'extinctions systématiques, qui se différencient par leurs effets dans l'espace réciproque : les extinctions intégrales, les extinctions zonales et les extinctions sérielles.

Extinctions et groupes d'espace

Pour déterminer une structure cristalline, la connaissance des conditions d'extinction est essentielle : elle permet l'identification des élements de symétrie translatoires du cristal (axes hélicoïdaux, miroirs translatoires) et ainsi la sélection d'un ensemble limité de groupes d'espace pouvant décrire sa symétrie. Pour cette raison, les tables internationales de cristallographie^[1] contiennent, pour chaque groupe d'espace, la liste des conditions de réflexion.

Certains groupes d'espace ne présentent aucune condition d'extinction, c'est-à-dire que toutes les réflexions sont autorisées : P1, P1, P2, Pm, P2/m, P222, Pmm2, Pmmm, P4, P4, P4/m, P422, P4mm, P42m, P4m2, P4/mmm, P3, P3, P312, P321, P3m1, P31m, P3m1, P31m, P6, P6, P6/m, P622, P6mm, P6m2, P62m, P6/mmm, P23, Pm3, P432, P43m et Pm3m.

Extinctions intégrales

Les extinctions intégrales concernent toutes les réflexions, d'indices $h k l$ , de l'espace réciproque. Elles ont lieu lorsque la maille du cristal n'est pas primitive, c'est-à-dire pour les réseaux de Bravais mC, oS, oI, oF, tI, hR, cI et cF.

Conditions d'extinction et conditions de réflexion intégrales
Maille	Réflexions	Vecteur de translation	Condition d'extinction	Condition de réflexion
Primitive	$h k l$	aucun	aucune	toutes
Face A centrée	$h k l$	$\vec{b}/2+\vec{c}/2$	$k + l = 2 n + 1$	$k + l = 2 n$
Face B centrée	$h k l$	$\vec{a}/2+\vec{c}/2$	$h + l = 2 n + 1$	$h + l = 2 n$
Face C centrée	$h k l$	$\vec{a}/2+\vec{b}/2$	$h + k = 2 n + 1$	$h + k = 2 n$
Centrée	$h k l$	$\vec{a}/2+\vec{b}/2+\vec{c}/2$	$h + k + l = 2 n + 1$	$h + k + l = 2 n$
À faces centrées	$h k l$	$\vec{b}/2+\vec{c}/2$ $\vec{a}/2+\vec{c}/2$ $\vec{a}/2+\vec{b}/2$	$h$ , $k$ et $l$ de parités différentes	$h$ , $k$ et $l$ de même parité
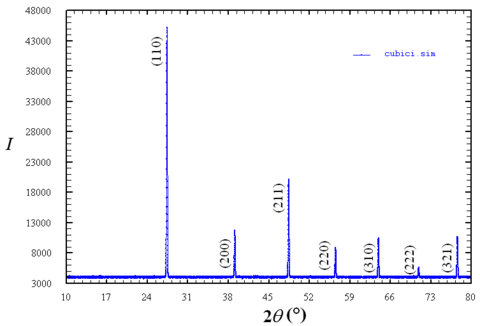
Rhomboédrique	$h k l$	$2\vec{a}/3+\vec{b}/3+\vec{c}/3$	$- h + k + l = 3 n$	$- h + k + l$ ≠ $3 n$

Effet des conditions d'extinction intégrales sur les diffractogrammes de poudre.

Diffractogramme poudre calculé pour un matériau fictif de maille cubique primitive. Les indices

h k l

sont donnés à gauche de chaque réflexion.

Diffractogramme poudre calculé pour un matériau fictif de maille cubique centrée. Les indices

h k l

sont donnés à gauche de chaque réflexion.

Diffractogramme poudre calculé pour un matériau fictif de maille cubique à faces centrées. Les indices

h k l

sont donnés à gauche de chaque réflexion.

Extinctions zonales

Les extinctions zonales ne concernent que les réflexions appartenant à certains plans de l'espace réciproque. Elles ont lieu lorsque des miroirs translatoires sont présents parmi les éléments de symétrie du cristal.

Conditions d'extinction et conditions de réflexion zonales
Miroir translatoire	Réflexions	Vecteur de translation	Condition d'extinction	Condition de réflexion
$a\perp\vec{b}$	$h 0 l$	$\vec{a}/2$	$h = 2 n + 1$	$h = 2 n$
$a\perp\vec{c}$	$h k 0$	$\vec{a}/2$	$h = 2 n + 1$	$h = 2 n$
$b\perp\vec{a}$	$0 k l$	$\vec{b}/2$	$k = 2 n + 1$	$k = 2 n$
$b\perp\vec{c}$	$h k 0$	$\vec{b}/2$	$k = 2 n + 1$	$k = 2 n$
$c\perp\vec{a}$	$0 k l$	$\vec{c}/2$	$l = 2 n + 1$	$l = 2 n$
$c\perp\vec{b}$	$h 0 l$	$\vec{c}/2$	$l = 2 n + 1$	$l = 2 n$
$n\perp\vec{a}$	$0 k l$	$\vec{b}/2+\vec{c}/2$	$k + l = 2 n + 1$	$k + l = 2 n$
$n\perp\vec{b}$	$h 0 l$	$\vec{a}/2+\vec{c}/2$	$h + l = 2 n + 1$	$h + l = 2 n$
$n\perp\vec{c}$	$h k 0$	$\vec{a}/2+\vec{b}/2$	$h + k = 2 n + 1$	$h + k = 2 n$
$d\perp\vec{a}$	$0 k l$	$\vec{b}/4\pm\vec{c}/4$	$k + l$ ≠ $4 n$	$k + l = 4 n$ , $k = 2 n$ , $l = 2 n$
$d\perp\vec{b}$	$h 0 l$	$\vec{a}/4\pm\vec{c}/4$	$h + l$ ≠ $4 n$	$h + l = 4 n$ , $h = 2 n$ , $l = 2 n$
$d\perp\vec{c}$	$h k 0$	$\vec{a}/4\pm\vec{b}/4$	$h + k$ ≠ $4 n$	$h + k = 4 n$ , $h = 2 n$ , $k = 2 n$

Extinctions sérielles

Les extinctions sérielles ne concernent que les réflexions appartenant à certaines droites de l'espace réciproque. Elles ont lieu lorsque des axes hélicoïdaux sont présents parmi les éléments de symétrie du cristal.

Conditions d'extinction et conditions de réflexion sérielles
Axe hélicoïdal	Réflexions	Vecteur de translation	Condition d'extinction	Condition de réflexion
$21$ , $42$ , $63$ // [100]	$h 00$	$\vec{a}/2$	$h = 2 n + 1$	$h = 2 n$
$21$ , $42$ , $63$ // [010]	$0 k 0$	$\vec{b}/2$	$k = 2 n + 1$	$k = 2 n$
$21$ , $42$ , $63$ // [001]	$00 l$	$\vec{c}/2$	$l = 2 n + 1$	$l = 2 n$
$31$ , $32$ , $62$ , $64$ // [100]	$h 00$	$\vec{a}/3,$ $2\vec{a}/3$	$h$ ≠ $3 n$	$h = 3 n$
$31$ , $32$ , $62$ , $64$ // [010]	$0 k 0$	$\vec{b}/3,$ $2\vec{b}/3$	$k$ ≠ $3 n$	$k = 3 n$
$31$ , $32$ , $62$ , $64$ // [001]	$00 l$	$\vec{c}/3,$ $2\vec{c}/3$	$l$ ≠ $3 n$	$l = 3 n$
$41$ , $43$ // [100]	$h 00$	$\vec{a}/4,$ $3\vec{a}/4$	$h$ ≠ $4 n$	$h = 4 n$
$41$ , $43$ // [010]	$0 k 0$	$\vec{b}/4,$ $3\vec{b}/4$	$k$ ≠ $4 n$	$k = 4 n$
$41$ , $43$ // [001]	$00 l$	$\vec{c}/4,$ $3\vec{c}/4$	$l$ ≠ $4 n$	$l = 4 n$
$61$ , $65$ // [100]	$h 00$	$\vec{a}/6,$ $5\vec{a}/6$	$h$ ≠ $6 n$	$h = 6 n$
$61$ , $65$ // [010]	$0 k 0$	$\vec{b}/6,$ $5\vec{b}/6$	$k$ ≠ $6 n$	$k = 6 n$
$61$ , $65$ // [001]	$001$	$\vec{c}/6,$ $5\vec{c}/6$	$l$ ≠ $6 n$	$l = 6 n$

Calcul des conditions d'extinction

Les conditions d'extinction pour un élément de symétrie translatoire donné se trouvent en cherchant les conditions sur les indices $h k l$ qui annulent systématiquement le facteur de structure :

$F(hkl) = \sum_{p=1}^m \sum_{j=1}^n f_j \cdot e^{2i\pi(hx_{j,p}+ky_{j,p}+lz_{j,p})} = \sum_{j=1}^n F_j(hkl) = 0$

où $f j$ est le facteur de diffusion atomique de l'atome $j$ de l'unité asymétrique de la maille, $x j, p$ , $y j, p$ , $z j, p$ sont ses coordonnées dans la maille en fonction de l'opération de symétrie $p$ et $F j (h k l)$ est sa contribution partielle au facteur de structure.

Pour cela, il suffit de considérer un atome $j$ en position générale : si pour cet atome

$F_j(hkl) = f_j \sum_{p=1}^m e^{2i\pi(hx_{j,p}+ky_{j,p}+lz_{j,p})} = 0,$

alors $F (h k l) = 0$ pour l'ensemble des atomes du cristal. Il suffit donc de résoudre l'équation

$\sum_{p=1}^m e^{2i\pi(hx_{j,p}+ky_{j,p}+lz_{j,p})} = 0$

en fonction de $h$ , $k$ et $l$ pour $x j, p$ , $y j, p$ , $z j, p$ quelconques.

Par exemple, pour une maille centrée :

$\begin{array}{rcl} F_j(hkl) & = & e^{2i\pi(hx_j+ky_j+lz_j)} + e^{2i\pi[h(x_j+1/2)+k(y_j+1/2)+l(z_j+1/2)]} \\[1ex] ~ & = & e^{2i\pi(hx_j+ky_j+lz_j)}(1+e^{2i\pi(h/2+k/2+l/2)}) \end{array}$

L'annulation du facteur de structure partiel de l'atome $j$ conduit à

$e^{2i\pi(h/2+k/2+l/2)}=-1,\,$

ce qui n'est possible que si $h / 2 + k / 2 + l / 2$ est un demi-entier : la somme $h + k + l$ doit être impaire pour que l'on ait une extinction.

Notes et références

(de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Auslöschung (Kristallographie) » (voir la liste des auteurs)

↑ (en) International Tables for Crystallography, vol. A : Space-group symmetry, Th. Hahn, Kluwer Academic Publishers, 2005 (réimpr. corrigée), 5^e éd. (ISBN 978-0-470-68908-0)

Bibliographie

(de) Dieter Schwarzenbach, Kristallographie, Springer, 2001 (ISBN 3-540-67114-5)

Catégorie :

Radiocristallographie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Condition d'extinction de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Extinction Des Espèces — Pour les articles homonymes, voir Extinction. Les mécanismes de l évolution biologique Mécanismes non aléatoires … Wikipédia en Français
Extinction d'espèces — Extinction des espèces Pour les articles homonymes, voir Extinction. Les mécanismes de l évolution biologique Mécanismes non aléatoires … Wikipédia en Français
Extinction des especes — Extinction des espèces Pour les articles homonymes, voir Extinction. Les mécanismes de l évolution biologique Mécanismes non aléatoires … Wikipédia en Français
Extinction De L'Holocène — Le dodo, un oiseau de l Île Maurice, s est éteint vers la fin du XVIIe siècle après que les hommes eurent détruit les forêts où les oiseaux faisaient leur nid et introduit des animaux qui mangeaient leurs œufs … Wikipédia en Français
Extinction de l'Holocene — Extinction de l Holocène Le dodo, un oiseau de l Île Maurice, s est éteint vers la fin du XVIIe siècle après que les hommes eurent détruit les forêts où les oiseaux faisaient leur nid et introduit des animaux qui mangeaient leurs œufs … Wikipédia en Français
Extinction de l'holocène — Le dodo, un oiseau de l Île Maurice, s est éteint vers la fin du XVIIe siècle après que les hommes eurent détruit les forêts où les oiseaux faisaient leur nid et introduit des animaux qui mangeaient leurs œufs … Wikipédia en Français
Extinction chess — is a variant of western Chess where the objective of the game has changed. Instead of the winning condition of the game being the checkmate of the opponent s king, the object of the game is to capture all of a particular kind of piece the… … Wikipedia
Extinction des espèces — Pour les articles homonymes, voir Extinction. Les mécanismes de l évolution biologique Mécanismes non aléatoires … Wikipédia en Français
Extinction de l'Holocène — Le dodo, un oiseau de l Île Maurice, s est éteint vers la fin du XVIIe siècle après que les hommes eurent détruit les forêts où les oiseaux faisaient leur nid et introduit des animaux qui mangeaient leurs œufs. L’extinction de l Holocène est … Wikipédia en Français
extinction — /ik stingk sheuhn/, n. 1. the act of extinguishing. 2. the fact or condition of being extinguished or extinct. 3. suppression; abolition; annihilation: the extinction of an army. 4. Biol. the act or process of becoming extinct; a coming to an end … Universalium

Dictionnaires et Encyclopédies sur 'Academic'

Condition d'extinction

Sommaire

Extinctions et groupes d'espace

Extinctions intégrales

Extinctions zonales

Extinctions sérielles

Calcul des conditions d'extinction

Notes et références

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Condition d'extinction

Sommaire

Extinctions et groupes d'espace

Extinctions intégrales

Extinctions zonales

Extinctions sérielles

Calcul des conditions d'extinction

Notes et références

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link