Composante fortement connexe
- Composante fortement connexe
-
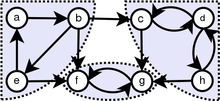
Décomposition d'un graphe en composantes fortement connexes
En théorie des graphes, une composante fortement connexe d'un graphe orienté G est un sous-graphe maximal de G tel que pour toute paire de sommets u et v dans ce sous-graphe, il existe un chemin de u à v et un chemin de v à u.
Un graphe est dit fortement connexe s'il est formé d'une seule composante fortement connexe. De manière générale, un graphe se décompose de manière unique comme union de composantes fortement connexes disjointes.
Graphe des composantes
À partir d'un graphe orienté G, le graphe G’ des composantes de G est défini de la manière suivante :
- les sommets de G’ sont les composantes fortement connexes de G ;
- pour toute arête (u, v) de G telle que u et v sont dans deux composantes distinctes U et V, on ajoute une arête de U à V dans G’.
Le graphe des composantes est toujours acyclique. Inversement, tout graphe acyclique est égal au graphe de ses composantes.
Algorithmes
Plusieurs algorithmes permettent de calculer la décomposition en composantes fortement connexes d'un graphe en temps linéaire :
Voir aussi
- Graphe connexe, la notion équivalente à la forte connexité pour les graphes non orientés.
- Théorème de Robbins (en)
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Composante fortement connexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Composante homopolaire — Triphasé Graphique des trois tensions de même fréquence/amplitude et déphasées de 120° Le triphasé est un système de trois tensions sinusoïdales de même fréquence et généralement de même amplitude qui sont déphasées entre elles (de 120 ° ou… … Wikipédia en Français
Graphe connexe — Sommaire 1 Définition 2 Propriétés 3 Algorithmes 4 Exemples 5 Voir aussi … Wikipédia en Français
SYSTÈMES DE TRANSFORMATIONS (THÉORIE DES) — Élaborée dans une optique interdisciplinaire, la théorie des systèmes de transformations propose un formalisme suffisamment général pour être applicable à des champs d’investigation que l’évolution des sciences, dans son mouvement vers une… … Encyclopédie Universelle
Algorithme de Tarjan — En théorie des graphes, l algorithme de Tarjan permet de déterminer les composantes fortement connexes d un graphe orienté[1]. Il porte le nom de son inventeur, Robert Tarjan. L algorithme de Tarjan est de complexité linéaire, comme l algorithme… … Wikipédia en Français
Graphe d'une chaîne de Markov — et classification des états Le graphe d une chaîne de Markov et la classification des états sont des notions de la théorie des graphes utilisées en calcul des probabilités. Sommaire 1 Graphe d une chaîne de Markov 2 Classification des états … Wikipédia en Français
Graphe d'une chaîne de Markov et classification des états — Le graphe d une chaîne de Markov et la classification des états sont des notions de la théorie des graphes utilisées en calcul des probabilités. Sommaire 1 Graphe d une chaîne de Markov 2 Classification des états 3 Lexi … Wikipédia en Français
Lexique de la théorie des graphes — Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Acyclique (grap … Wikipédia en Français
Graphe partiel — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A … Wikipédia en Français
Lexique (graphe) — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A … Wikipédia en Français
Lexique De La Théorie Des Graphes — Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A … Wikipédia en Français

