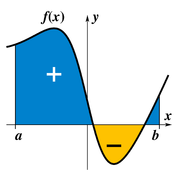
∫

Pour les articles homonymes, voir intégration.

L'intégration est un concept fondamental en mathématiques, issu du calcul des aires et de l'analyse, et utilisé dans de nombreuses branches des mathématiques. L'intégration permet, entre autres, à partir d'une fonction ƒ, de donner une mesure de l'espace délimité par la représentation graphique de ƒ.

Les opérations de mesure de grandeurs (longueur d'une courbe, aire, volume, flux...) et de calcul de probabilités étant souvent soumises à des calculs d'intégrales, l'intégration est un outil scientifique fondamental^[1]. C'est la raison pour laquelle l'intégration est souvent abordée dès l'enseignement secondaire.

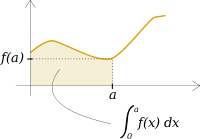
Définition du cas réel à partir de l'aire sous la courbe

Représentation graphique d'un intégrande ƒ positive et de son intégrale.

Représentation graphique d'un intégrande ƒ réelle et de son intégrale (avec signe)

Si ƒ est une fonction réelle positive continue prenant ses valeurs dans un segment I = [0,a], alors l'intégrale de ƒ sur