- ∪
-
Union (mathématiques)
Définition
Dans la théorie des ensembles, l'union ou réunion de deux ensembles A et B est l'ensemble qui contient tous les éléments qui appartiennent à A ou appartiennent à B. On note l'union de A et B A ∪ B. En notation symbolique, c'est :
Par exemple l'union des ensembles A={1,2,3} et B={2,3,4} est l'ensemble {1,2,3,4}.
En algèbre booléenne, l'union est associée à l'opérateur logiqueou inclusif.On généralise ce concept à une famille d'ensembles
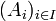 . La réunion ou union des ensembles membres de cette famille est l'ensemble des éléments x pour lesquels il existe un
. La réunion ou union des ensembles membres de cette famille est l'ensemble des éléments x pour lesquels il existe un 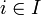 tel que
tel que 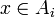 . On le note alors
. On le note alors 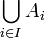 .
.Propriétés algébriques
- L'union est associative, i.e. pour des ensembles A, B et C quelconques, on a :
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
- L'union est commutative, i.e. pour des ensembles A et B quelconques, on a :
- A ∪ B = B ∪ A
- L'intersection est distributive sur l'union, i.e. pour des ensembles A, B et C quelconques, on a :
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- Portail des mathématiques
Catégories : Théorie des ensembles | Opération
Wikimedia Foundation. 2010.


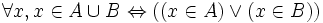

 Union
Union

 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit