État nématique

État nématique

Nématique

Texture dans une phase nématique.

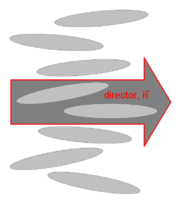
L'état nématique est un état de la matière intermédiaire entre les phases solide cristalline et liquide. Les molécules, de forme allongée, sont réparties sans ordre de position (comme dans un liquide) mais en demeurant en moyenne parallèles les unes aux autres, c'est-à-dire avec un ordre d'orientation à longue portée (comme dans un cristal).

Sommaire

Généralités

Orientation moyenne des molécules et directeur n.

Les molécules composant le nématique ont une forme cylindrique, la plupart des propriétés caractéristiques des nématiques en découle. Ainsi, le fluide nématique diffère du liquide isotrope par l'alignement spontané des molécules. La phase nématique naît de cet ordre d'orientation des molécules à grande distance, c'est un comportement collectif. L'orientation moyenne des molécules est appelée le directeur 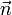\vec{n} et est définie à π près[A 1].

La substance est biréfringente, optiquement uniaxe positif. L'observation d'un échantillon au microscope montre des fils à l'intérieur. En référence à ces défauts, observés dans les fluides cristallins de O. Lehman, G. Friedel nomma cette phase « nématique » (du grec νεμα « fil »)[1].

Si la viscosité de la phase nématique est du même ordre de grandeur que celle de la phase liquide isotrope, une forte anisotropie existe, la substance coule plus facilement lorsque l'écoulement est dans le sens du directeur que lorsqu'il est dans un plan perpendiculaire[2]. Dans ce dernier cas, l'écoulement peut tendre à modifer l'orientation du directeur. L'étude de l'écoulement d'un nématique sous contrainte est appelée nématodynamique.

Le diagramme de phase classique est modifié, la phase nématique s'intercalant entre la phase liquide et la phase solide (ou/et une phase smectique le cas échéant), certaines substances possédant un point triple liquide-nématique-solide et d'autres susceptibles d'accepter la phase nématique pour une pression nulle[B 1].

Distorsions

Distribution de l'orientation des molécules.

L'ordre d'orientation se mesure en général à partir du paramètre d'ordre 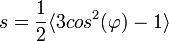s = \frac{1}{2} \langle 3 cos^2(\varphi) -1\rangle où φ est l'angle d'une molécule avec le directeur et la mise entre crochet indique le calcul de la valeur moyenne sur un grand nombre de molécules[B 2]. À l'instar de la fonction de distribution, cette fonction possède une symétrie cylindrique suivant le directeur. Dans un liquide isotrope, aucune direction n'est privilégiée, on obtient s=0. Dans le cas d'une parallélité parfaite des molécules, on aurait s=1.

L'énergie libre ne dépend pas de la direction d'orientation moyenne (c'est par exemple l'ancrage aux surfaces qui donne une direction privilégiée). Si l'orientation du directeur varie d'une région à l'autre du nématique, cela induit une distorsion et une augmentation de l'énergie libre.

L'expression d'Oseen-Frank permet de traduire l'énergie libre en fonction des distorsions spatiales des molécules dans le nématique. L'expression comprend quatre termes qui dépendent de l'orientation du directeur, cependant, le quatrième terme, dit « de surface » est négligé dans la majorité des cas. L'expression de l'énergie libre par unité de volume s'écrit[A 2],[B 3] :

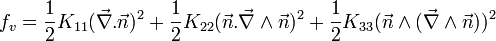f_{v} = \frac{1}{2} K_{11} (\vec{\nabla}.\vec{n})^2 + \frac{1}{2} K_{22} (\vec{n}.\vec{\nabla}\wedge\vec{n})^2 + \frac{1}{2} K_{33} (\vec{n}\wedge(\vec{\nabla}\wedge\vec{n}))^2 .

Le premier terme splay traduit les déformations en éventail du directeur, le second terme twist traduit les déformations en torsion du directeur, le troisième terme bend, traduit les déformations en courbure du directeur.

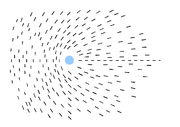
Disinclinaisons

Les fils observés au microscope dans les nématiques sont des lignes de dislocation dans le fluide. Pour comprendre les disinclinaisons, il est possible d'utiliser l'approximation d'élasticité isotrope, on pose alors K11 = K22 = K33 = K.

L'expression de l'énergie libre se simplifie et devient :

Disposition des molécules dans le cas m=-1/2
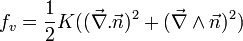f_{v} = \frac{1}{2} K ((\vec{\nabla}.\vec{n})^2 + (\vec{\nabla}\wedge\vec{n})^2).

On considère une ligne de disinclinaison le long de l'axe z, le directeur étant contraint dans le plan (x,y), il fait un angle θ(x,y) avec l'axe x. Dans ce référentiel, le directeur 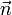\vec{n} a pour coordonnées (cos(θ), sin(θ),0).

L'expression se calcule alors en fonction de θ[A 3],[B 4] :

f_{v} = \frac{1}{2} K \left[\left(\frac{\partial n_{x}}{\partial x} + \frac{\partial n_{y}}{\partial y}\right)^2 + \left(\frac {\partial n_{y}}{\partial x} - \frac {\partial n_{x}}{\partial y}\right)^2\right]=\frac{1}{2} K \left[\left(\frac {\partial \theta}{\partial x}\right)^2+ \left(\frac {\partial \theta}{\partial y}\right)^2\right] = \frac{1}{2} K [\vec{\nabla}\theta]^2.

Disposition des molécules dans le cas m=1/2

Cette énergie libre est minimale lorsque[3] Δθ = 0.

Les solutions θ=constante correspondent à un champ uniforme. Les solutions sont du type θ= m φ + constante où tg(φ) = y / x avec m entier ou demi-entier (car le directeur est défini à π près)[A 4],[B 5], la constante correspondant à une rotation du directeur. Cette équation permet de tracer les configurations du directeur correspondant aux différentes disinclinaisons observées, avec une singularité au centre[B 6].

L'énergie par unité de longueur de la distorsion s'écrit finalement :

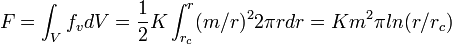F = \int_{V} f_{v} dV = \frac{1}{2} K \int_{r_{c}}^r (m/r)^2 2\pi rdr=Km^2\pi ln(r/r_{c}) où rc est le rayon de coupure[A 5] (de l'ordre de la dimension moléculaire) que l'on peut estimer en comparant l'énergie du nématique à celle de la phase isotrope. De plus, comme l'énergie libre dépend de m², les configurations avec m petit sont plus favorables.

Orientation en présence d'un champ électrique

L'anisotropie diélectrique[4] dans les nématiques est à l'origine de la plupart des applications électrico-optiques. Les molécules composant le nématique sont particulièrement sensibles aux champs électromagnétiques. Elles portent un moment dipolaire (induit par le champ et/ou permanent, provenant de la différence de répartition des charges positives et négatives au sein de la molécule). En fonction de la valeur des coefficients de permittivité, les molécules tendent à s'orienter parallèlement ou perpendiculairement au champ électrique 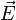\vec{E} et créent un champ de polarisation. Le champ de polarisation 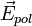\vec{E}_{pol} des molécules alignées contrebalance, en partie, le champ initial 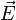\vec{E} (comme dans un condensateur en présence d'un diélectrique).

Si on identifie l'axe z avec celui du directeur, la matrice des constantes diélectriques s'écrit[5] :

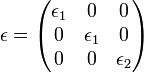{\epsilon}=\begin{pmatrix} \epsilon_{1} &0 & 0\\ 0 & \epsilon_{1} & 0\\ 0 & 0 &\epsilon_{2}\\ \end{pmatrix} où ε2 est la constante diélectrique dans l'axe de la molécule (id. axe z ou axe du directeur).

Le vecteur polarisation s'écrit (approximation du premier ordre) :

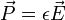
\vec{P} = {\epsilon} \vec{E}

ou (suivant ses composantes) :

Pi = ∑ εijEj
j

où le champ 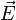\vec{E} possède des composantes Ex, Ey, Ez. Notons que le champ 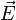\vec{E} n'est pas nécessairement aligné avec le vecteur polarisation (anisotropie : ε1≠ ε2), ni initialement avec la molécule.

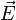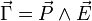Le couple exercé sur le directeur par le champ \vec{E} est : \vec{\Gamma} = \vec{P} \wedge \vec{E} .

Les composantes du couple sont donc : (Γx = (ε1 − ε2)EyEz, Γy = (ε2 − ε1)ExEz, Γz = 0). Si la différence ε2 − ε1 est négative, le couple tend à aligner le directeur perpendiculairement au champ, si elle est positive, le directeur tend à s'aligner au champ.

Bibliographie

Notes et références

  1. ↑ G. Friedel, Les états mésomorphes de la matière. Annales de physique 18, S. 273–474, 1922
  2. ↑ M. Miesowicz, Influence of a Magnetic Field on the Viscosity of Para-Azoxyanisol. Nature 136, 261 (17 August 1935)[1]
  3. ↑ F. C. Frank, Discuss. Faraday Soc. 25, 19 (1958)
  4. ↑ Note : l'anisotropie diélectrique est directement liée aux propriétés optiques biréfringentes de la substance.
  5. ↑ P. Collings et M. Hird, Introduction to liquid crystals, Taylor & Francis , 1997 pages 19 et 195

P.G. de Gennes et J. Prost 1993

  1. ↑ page 11 propriétés générales des nématiques
  2. ↑ page 102 expression de Frank
  3. ↑ page 170 énergie libre d'une disinclinaison
  4. ↑ page 171 valeurs de m
  5. ↑ page 171 énergie libre d'une disinclinaison

S. Chandrasekhar 1992

  1. ↑ page 27 diagrammes de phases
  2. ↑ page 38 paramètre d'ordre s
  3. ↑ page 116 expression de Frank
  4. ↑ page 118 énergie libre d'un disinclinaison
  5. ↑ page 118 valeurs de m
  6. ↑ page 119 images de singularités

Liens internes

Liens externes

  • Portail de la physique Portail de la physique
Ce document provient de « N%C3%A9matique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article État nématique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Etat nematique — Nématique Texture dans une phase nématique. L état nématique est un état de la matière intermédiaire entre les phases solide cristalline et liquide. Les molécules, de forme allongée, sont réparties sans ordre de position (comme dans un liquide)… …   Wikipédia en Français

  • État mésomorphe — Nématique Texture dans une phase nématique. L état nématique est un état de la matière intermédiaire entre les phases solide cristalline et liquide. Les molécules, de forme allongée, sont réparties sans ordre de position (comme dans un liquide)… …   Wikipédia en Français

  • nématique — ● nématique adjectif Se dit de l état mésomorphe, plus voisin de l état liquide que de l état cristallisé, dans lequel les molécules, de forme allongée, peuvent se déplacer librement mais restent parallèles entre elles, formant ainsi un liquide… …   Encyclopédie Universelle

  • État cholestérique — ● État cholestérique variante de l état nématique, obtenue avec des molécules optiquement actives et caractérisée par une superstructure en hélice, qui diffracte la lumière et donne des couleurs remarquables …   Encyclopédie Universelle

  • Nématique — Texture dans une phase nématique. L état nématique est un état de la matière intermédiaire entre les phases solide cristalline et liquide. Les molécules, de forme allongée, sont réparties sans ordre de position (comme dans un liquide) mais en… …   Wikipédia en Français

  • MÉSOMORPHE (ÉTAT) — L’état mésomorphe présente une organisation intermédiaire entre celle d’un solide monocristallin et celle d’un liquide. Les phases solides ont une périodicité tridimensionnelle stricte alors que, dans les liquides usuels, ni la direction des… …   Encyclopédie Universelle

  • LIQUIDE (ÉTAT) — La notion de liquide est une notion familière, l’état liquide étant, avec l’état solide et l’état gazeux, l’un des trois états communs de la matière. On peut étudier un liquide comme une phase condensée fluide. Cela signifie que le liquide a une… …   Encyclopédie Universelle

  • PHASE (TRANSITIONS DE) — Les premières transitions de phase observées ont été des changements d’état tels que la fusion de la glace ou la vaporisation de l’eau. Lors d’un changement d’état, le système, au sens de la thermodynamique, se présente comme la réunion de deux… …   Encyclopédie Universelle

  • CRISTAUX LIQUIDES - Phases mésomorphes biologiques — Dans les substances organiques, il existe plusieurs types de cristaux liquides (myéliniques, smectiques, nématiques). Ceux de type cholestérique ont des propriétés optiques remarquables: pouvoir rotatoire considérable et réflexion de lumière… …   Encyclopédie Universelle

  • némat- — némat(o) ♦ Élément, du gr. nêma, nêmatos « fil ». ⇒NÉM(O) , NÉMAT(O) , (NÉM , NÉMO , NÉMAT , NÉMATO )élém. formant I. Ném(o) , némat(o) [élém. tiré du gr. , «fil» et entrant dans la constr. de mots sav. appartenant principalement au vocab. de la… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”