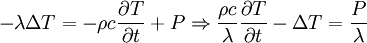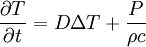Établissement de l'équation de conduction de la chaleur

Équation de la chaleur

En mathématiques et en physique théorique, l'équation de la chaleur est une équation aux dérivées partielles parabolique, introduite initialement en 1811 par Fourier pour décrire le phénomène physique de conduction thermique.

Sommaire

1 Équation de la chaleur
2 Établissement de l'équation de la chaleur
3 Autres phénomènes physiques
4 Généralisations
5 Articles liés
6 Bibliographie
7 Notes

Équation de la chaleur

Soit 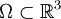$\Omega \subset \mathbb R^3$ un domaine à bord 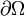$\partial \Omega$ . Soit T(x,t) le champ de température sur ce domaine. En l'absence des sources thermiques^[1] dans le domaine, l'équation de la chaleur s'écrit :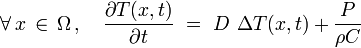

$\forall \, x \, \in \, \Omega \, , \quad \frac{\partial T (x,t)}{\partial t} \ = \ D \ \Delta T(x,t) + \frac{P}{\rho C}$

où $Δ$ est l'opérateur Laplacien, D est le cœfficient de diffusivité thermique et P une éventuelle production volumique de chaleur propre. Pour que le problème soit mathématiquement bien posé, il faut en général spécifier :

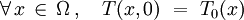une condition initiale : $\forall \, x \, \in \, \Omega \, , \quad T (x,0) \ = \ T_0(x)$ ;
une condition aux limites sur le bord du domaine, par exemple :
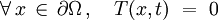- Dirichlet : $\forall \, x \, \in \, \partial \Omega \, , \quad T (x,t) \ = \ 0$ ;
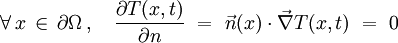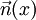- ou Neumann : $\forall \, x \, \in \, \partial \Omega \, , \quad \frac{\partial T (x,t)}{\partial n} \ = \ \vec{n}(x) \cdot \vec{\nabla} T(x,t) \ = \ 0$ , où $\vec{n}(x)$ est le vecteur normal unitaire au point x.

Établissement de l'équation de la chaleur

Il existe plusieurs approches, par exemple le bilan pour un volume de contrôle. On suit ici un raisonnement s'appuyant sur la thermodynamique et la loi de Fourier.

Appliquons le premier principe de la thermodynamique à un volume $τ$ de conducteur contenu à l'intérieur d'une surface $Σ$ entre $t$ et $t + d t$ :

U (t + d t) - U (t) = δ W + δ Q

on considère ici un système isochore par conséquent $δ W = 0$ . De plus,

$U(t) = \iiint_\tau \rho c T(t) \mathrm{d}\tau + f(V)$

où $ρ$ est la masse volumique du matériau (en kg/m³), $c$ la chaleur spécifique massique du matériau (en J/kg.K) et $f (V)$ est une fonction du volume. Alors

$U(t+\mathrm{d}t)-U(t)=\iiint_\tau \rho c (T(t+\mathrm{d}t)-T(t)) \mathrm{d}\tau = \iiint_\tau \rho c \frac{\partial T}{\partial t} \mathrm{d}t \mathrm{d}\tau$

On a aussi, par définition de 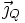$\vec{\jmath}_{Q}$ (vecteur densité de flux de chaleur) et de la densité volumique de source de chaleur par unité de temps P (en W/m³) :

(note pour le signe : 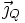$\vec{\jmath}_{Q}$ est positif quand le flux est vers l'extérieur, donc la variation de chaleur est alors négative dans le volume)

$\delta Q = - \left(\oint_{\Sigma} \vec\jmath_{Q}\cdot\mathrm{d}\vec{S}\right)\mathrm{d}t+\left(\iiint_\tau P\mathrm{d}\tau\right)\mathrm{d}t$

Avec le théorème de Green-Ostrogradsky on obtient :

$\delta Q = - \left(\iiint_\tau \operatorname{div} \vec\jmath_{Q} \mathrm{d}\tau\right)\mathrm{d}t+\left(\iiint_\tau P\mathrm{d}\tau\right)\mathrm{d}t$

donc :

$\iiint_\tau \rho c \frac{\partial T}{\partial t} \mathrm{d}t \mathrm{d}\tau = - \iiint_\tau \operatorname{div}\vec\jmath_{Q} \mathrm{d}\tau \mathrm{d}t+\iiint_\tau P\mathrm{d}\tau \mathrm{d}t$

or ceci est valable pour tout volume $τ$ , donc :

$\operatorname{div} \vec\jmath_{Q} = - \rho c \frac{\partial T}{\partial t} + P$

En utilisant la loi de Fourier :

$\vec\jmath_{Q} = - \lambda \overrightarrow\operatorname{grad}T$

et le fait que :

$\operatorname{div}\left(\overrightarrow\operatorname{grad}\right) = \nabla^2 = \Delta$ (laplacien)

on obtient :

$-\lambda\Delta T= - \rho c\frac{\partial T}{\partial t} + P \Rightarrow \frac{\rho c}{\lambda}\frac{\partial T}{\partial t}-\Delta T=\frac{P}{\lambda}$

ce qui est bien l'équation de la chaleur.

Enfin, en posant 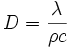$D = \frac{\lambda}{\rho c}$ (coefficient de diffusion).

$\frac{\partial T}{\partial t}=D\Delta T + \frac{P}{\rho c}$

Autres phénomènes physiques

Il est intéressant de remarquer que l'équation de la chaleur, introduite initialement pour décrire la conduction thermique, apparaît également dans d'autres branches de la physique théorique. Elle permet par exemple de décrire :

le phénomène de diffusion ;
certains aspects probabilistes du mouvement brownien ;

Enfin, il existe un lien avec la mécanique quantique non-relativiste : l'équation de la chaleur apparait en effet comme une équation de Schrödinger en temps imaginaire. Loin d'être une simple curiosité, cette propriété autorise des développements intéressants, car il est souvent plus facile mathématiquement de travailler avec l'équation de la chaleur qu'avec l'équation de Schrödinger.

Généralisations

L'équation de la chaleur s'étend naturellement :

dans 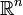$\mathbb R^n$ pour n quelconque ;
sur une variété riemannienne de dimension quelconque en introduisant l'opérateur de Laplace-Beltrami, qui généralise le Laplacien.

Bibliographie

Joseph Fourier ; Théorie analytique de la chaleur, Firmin Didot Père et Fils (Paris-1822). Réédition Jacques Gabay (1988), ISBN 2-87647-046-2.
Jean Dhombres & Jean-Bernard Robert ; Fourier, créateur de la physique mathématique, collection « Un savant, une époque », Belin (1998), ISBN 2-7011-1213-3.

Notes

↑ Par exemple, une source radioactive qui serait placée à l'intérieur du domaine, ... Il est possible d'introduire de telles sources d'énergie locales en ajoutant un terme à l'équation ; cf. l'article conduction thermique.

autre démonstration (ENS)

Portail des mathématiques
Portail de la physique

Ce document provient de « %C3%89quation de la chaleur ».

Catégories : Équation aux dérivées partielles | Physique mathématique | Thermodynamique | Transfert thermique | Loi en physique

Wikimedia Foundation. 2010.

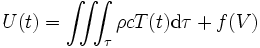
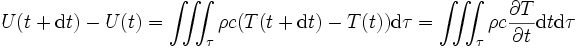
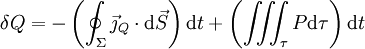
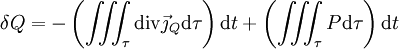
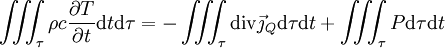
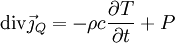
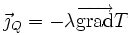
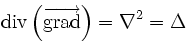Contenu soumis à la licence CC-BY-SA. Source : Article Établissement de l'équation de conduction de la chaleur de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Conduction Thermique — La conduction thermique (ou diffusion thermique) est un mode de phénomène de transfert thermique provoqué par une différence de température entre deux régions d un même milieu, ou entre deux milieux en contact, et se réalisant sans déplacement… … Wikipédia en Français
Conduction thermique — La conduction thermique (ou diffusion thermique) est un mode de transfert thermique provoqué par une différence de température entre deux régions d un même milieu, ou entre deux milieux en contact, et se réalisant sans déplacement global de… … Wikipédia en Français
Diffusion de la chaleur — Conduction thermique La conduction thermique (ou diffusion thermique) est un mode de phénomène de transfert thermique provoqué par une différence de température entre deux régions d un même milieu, ou entre deux milieux en contact, et se… … Wikipédia en Français
Equation de la chaleur — Équation de la chaleur En mathématiques et en physique théorique, l équation de la chaleur est une équation aux dérivées partielles parabolique, introduite initialement en 1811 par Fourier pour décrire le phénomène physique de conduction… … Wikipédia en Français
Équation de la chaleur — En mathématiques et en physique théorique, l équation de la chaleur est une équation aux dérivées partielles parabolique, introduite initialement en 1811 par Fourier pour décrire le phénomène physique de conduction thermique. Sommaire 1 Équation… … Wikipédia en Français
Diffusion thermique — Conduction thermique La conduction thermique (ou diffusion thermique) est un mode de phénomène de transfert thermique provoqué par une différence de température entre deux régions d un même milieu, ou entre deux milieux en contact, et se… … Wikipédia en Français
Loi de Fourier — Conduction thermique La conduction thermique (ou diffusion thermique) est un mode de phénomène de transfert thermique provoqué par une différence de température entre deux régions d un même milieu, ou entre deux milieux en contact, et se… … Wikipédia en Français
GLACIERS — Le mot glacier, comme la plupart de ses équivalents étrangers, a deux sens. Il désigne une masse de glace d’un seul tenant, permanente à l’échelle d’une vie humaine, avec le névé et la neige qui la recouvrent en partie, et les moraines mouvantes… … Encyclopédie Universelle
AÉRODYNAMIQUE — L’aérodynamique, dont l’étymologie évoque immédiatement l’action de l’air en mouvement, est la science qui étudie les différents aspects de cette action, notamment les forces, pressions et moments qui résultent du déplacement des corps dans… … Encyclopédie Universelle
ÉLECTROPHYSIOLOGIE — Les êtres vivants, végétaux et animaux, sont communément le siège de phénomènes électriques intimement liés aux activités vitales, dont ils sont un des aspects les plus révélateurs. On met ces phénomènes en évidence à l’aide d’électrodes… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Établissement de l'équation de conduction de la chaleur

Équation de la chaleur

Sommaire

Équation de la chaleur

Établissement de l'équation de la chaleur

Autres phénomènes physiques

Généralisations

Articles liés

Bibliographie

Notes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Établissement de l'équation de conduction de la chaleur

Équation de la chaleur

Sommaire

Équation de la chaleur

Établissement de l'équation de la chaleur

Autres phénomènes physiques

Généralisations

Articles liés

Bibliographie

Notes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link