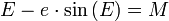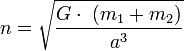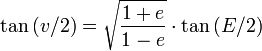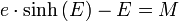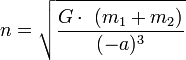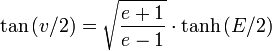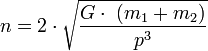Équation de kepler

Équation de Kepler

En astronomie, l'équation de Kepler est une formule liant l'excentricité e et l'anomalie excentrique E à l'anomalie moyenne M. L'importance de cette équation est qu'elle permet de passer de paramètres dynamiques du mouvement d'un astre (l'anomalie moyenne) a les paramètres géométriques (l'anomalie excentrique).

Sa démonstration est simple et fait appel au calcul de l'aire d'un secteur d'ellipse, dont le sommet est occupé par un des deux foyers, par deux méthodes différentes, dont l'une faisant appel à la loi des aires et l'autre en calculant l'aire de ce secteur elliptique projeté sur le cercle principal de l'ellipse. On obtient alors après simplification, en sachant que T est la période orbitale :

$E - e \cdot \sin{(E)} = M$

avec l'anomalie moyenne M définie par:

$M = n \cdot (t-t_0)$

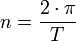
avec n le moyen mouvement : $n = \frac {2 \cdot \pi} {T}$

t le temps et t₀ étant l'instant du passage au périastre. L'anomalie moyenne peut être aussi exprimée par:

$n = \sqrt{\frac{G \cdot\ (m_1 + m_2)} {a^3}}$

G la constante universelle de la gravitation

m₁ et m₂ les masse des deux corps

a le demi grand axe de l'ellipse 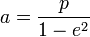$a = \frac{p} {1-e^2}$ ; p étant le paramètre de l'ellipse

L'équation de Kepler, associé au lien entre l'anomalie excentrique E et l'anomalie vraie v

$\tan{(v/2)} = \sqrt{\frac{1+e}{1-e}} \cdot \tan{(E/2)}$

permet de déterminer la position au cours du temps, d'un astre sur son orbite.

En cas d'orbite hyperbolique (e>1), on peut démontrer analytiquement une relation équivalente à l'équation de Kepler:

$e \cdot \sinh{(E)}- E = M$

M est défini de la même manière que dans le cas elliptique, avec l'expression du moyen mouvement suivant:

$n = \sqrt{\frac{G \cdot\ (m_1 + m_2)} {(-a)^3}}$

L'argument E n'est plus un angle comme c'est le cas dans le mouvement elliptique. E est dans ce cas liée à l'anomalie vraie v par:

$\tan{(v/2)} = \sqrt{\frac{e+1}{e-1}} \cdot \tanh{(E/2)}$

l'équation de kepler n'est pas définie dans le cadre du mouvement parabolique (e=1). Elle est remplacée par l'équation de Barker.

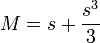$M = s + \frac{s^3}{3}$ (cette équation pouvant être résolue de manière analytique par la méthode de Cardan)

avec

s = tan(v / 2)

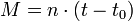$M = n \cdot (t-t_0)$ et

$n = 2 \cdot \sqrt{\frac{G \cdot\ (m_1 + m_2)} {p^3}}$

Par un changement judicieux de variable, les équations de Kepler elliptiques, paraboliques et hyperboliques peuvent être regroupées en une seule équation "universelle".

Voir aussi

Portail de l’astronomie

Ce document provient de « %C3%89quation de Kepler ».

Catégories : Mécanique céleste | Équation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation de kepler de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Equation de Kepler — Équation de Kepler En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer de paramètres dynamiques du mouvement d… … Wikipédia en Français
Équation de Kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer des paramètres dynamiques du mouvement d un astre (l… … Wikipédia en Français
Resolution de l'equation de Kepler — Résolution de l équation de Kepler Dans le mouvement keplerien, l équation de Kepler relie l anomalie moyenne M = nt à l anomalie excentrique E par l équation où e est l excentricité de la planète. Résoudre cette équation, c est trouver… … Wikipédia en Français
Résolution de l'équation de Kepler — Dans le mouvement keplerien, l équation de Kepler relie l anomalie moyenne M = nt à l anomalie excentrique E par l équation où e est l excentricité de la planète. Résoudre cette équation, c est trouver E(e,M) : comme série de Fourier puisque … Wikipédia en Français
Résolution de l'équation de kepler — Dans le mouvement keplerien, l équation de Kepler relie l anomalie moyenne M = nt à l anomalie excentrique E par l équation où e est l excentricité de la planète. Résoudre cette équation, c est trouver E(e,M) : comme série de Fourier puisque … Wikipédia en Français
Equation du centre — Équation du centre En astronomie, l’équation du centre traduit, dans le cadre du mouvement elliptique , la différence entre l anomalie vraie v et l anomalie moyenne M. Dans le cas du mouvement keplerien (deux astres tournant seuls, l un autour de … Wikipédia en Français
Équation du centre — En astronomie, l’équation du centre traduit, dans le cadre du mouvement elliptique, la différence entre l anomalie vraie v et l anomalie moyenne M. Dans le cas du mouvement keplerien (deux astres tournant seuls, l un autour de l autre) cette… … Wikipédia en Français
Kepler (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Pour l’article homophone, voir Keppler. Kepler peut vouloir désigner : Sommaire … Wikipédia en Français
Equation du temps — Équation du temps Sommaire 1 Définition 2 Allure de l évolution de l équation du temps 2.1 Analemme 2.2 Allure … Wikipédia en Français
Kepler's laws of planetary motion — In astronomy, Kepler s Laws of Planetary Motion are three mathematical laws that describe the motion of planets in the Solar System. German mathematician and astronomer Johannes Kepler (1571–1630) discovered them.Kepler studied the observations… … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Équation de kepler