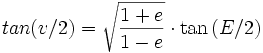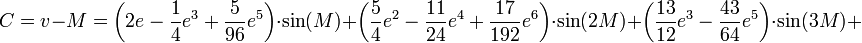Equation du centre

Equation du centre

Équation du centre

En astronomie, l’équation du centre traduit, dans le cadre du mouvement elliptique , la différence entre l'anomalie vraie v et l'anomalie moyenne M.

Dans le cas du mouvement keplerien (deux astres tournant seuls, l'un autour de l'autre) cette différence est périodique, de période T égale à la période de révolution du corps orbitant autour de l'astre central. L'équation du centre s'obtient à partir de deux équations qui mettent en jeu un autre argument qui est l'anomalie excentrique E :

E - e \cdot \sin{(E)} = M (équation de Kepler)
tan{(v/2)} = \sqrt{\frac{1+e}{1-e}} \cdot \tan{(E/2)}

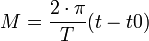
L'équation du centre vaut C = v − M avec M=\frac{2\cdot\pi}{T}(t-t0)

t et t0 sont respectivement le temps et l'instant du passage au périastre.

Pour calculer l'équation du centre pour une date donnée, il est nécessaire de résoudre l'équation de Kepler.

Lorsque l'excentricité e de l'orbite est faible, on peut approcher l'équation du centre par un développement limité, et ainsi éviter la résolution de l'équation de Kepler. On trouve en retenant les termes jusqu'à e6:

C=v-M=\left(2e-\frac{1}{4}e^3+\frac{5}{96}e^5\right)\cdot\sin(M)+\left(\frac{5}{4}e^2-\frac{11}{24}e^4+\frac{17}{192}e^6\right)\cdot\sin(2M)+\left(\frac{13}{12}e^3-\frac{43}{64}e^5\right)\cdot\sin(3M)+

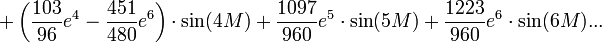
+\left(\frac{103}{96}e^4-\frac{451}{480}e^6\right)\cdot\sin(4M)+\frac{1097}{960}e^5\cdot\sin(5M)+\frac{1223}{960}e^6\cdot\sin(6M)...

L'obtention de ce développement limité est laborieux et fait appel aux fonctions de Bessel de premier espèce.

  • Portail de l’astronomie Portail de l’astronomie
Ce document provient de « %C3%89quation du centre ».

Wikimedia Foundation. 2010.

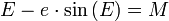Contenu soumis à la licence CC-BY-SA. Source : Article Equation du centre de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Équation du centre — En astronomie, l’équation du centre traduit, dans le cadre du mouvement elliptique, la différence entre l anomalie vraie v et l anomalie moyenne M. Dans le cas du mouvement keplerien (deux astres tournant seuls, l un autour de l autre) cette… …   Wikipédia en Français

  • Equation du temps — Équation du temps Sommaire 1 Définition 2 Allure de l évolution de l équation du temps 2.1 Analemme 2.2 Allure …   Wikipédia en Français

  • Equation de Kepler — Équation de Kepler En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer de paramètres dynamiques du mouvement d… …   Wikipédia en Français

  • Équation de kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer de paramètres dynamiques du mouvement d un astre (l… …   Wikipédia en Français

  • Équation du temps — L’équation du temps est un paramètre utilisé en astronomie pour rendre compte du mouvement apparent relatif du Soleil par rapport au soleil moyen, lesquels peuvent différer l un par rapport à l autre de plus ou moins un quart d heure environ. D… …   Wikipédia en Français

  • Équation de Kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer des paramètres dynamiques du mouvement d un astre (l… …   Wikipédia en Français

  • équation — (é koua sion) s. f. 1°   Terme d algèbre. Formule de l égalité établie entre deux quantités. Équation du premier degré, du second degré. Équation différentielle. Les racines d une équation. •   En tirant la racine d une équation cubique, DESC.… …   Dictionnaire de la Langue Française d'Émile Littré

  • Equation de Lane-Emden — Équation de Lane Emden En astrophysique, l équation de Lane Emden décrit la structure d un objet dont l équation d état est celle d un polytrope, et qui est soumis à l influence de son propre champ gravitationnel. Il est de plus supposé que l… …   Wikipédia en Français

  • Equation cartesienne — Équation cartésienne Dans un plan (cartésien), rapporté à un repère cartésien, les solutions d une équation E d inconnues x et y peuvent être interprétées comme un ensemble de points de ce plan. Quand ces solutions forment une courbe, on dit que… …   Wikipédia en Français

  • Equation de Poisson — Équation de Poisson Pour les articles homonymes, voir Poisson (homonymie). Articles d analyse vectorielle …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”