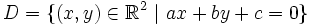Équation d'une droite

Équation d'une droite

Équation de droite

Sommaire

Définition

L'équation d'une droite D est une (ou plusieurs) équation(s) du premier degré à plusieurs inconnues (des coordonnes), et dont l'ensemble des solutions forment la droite D.

Dans le plan

Dans le plan, l'ensemble des points 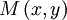M\left(x,y\right) formant D peut se représenter par une équation de la forme :

ax + by + c = 0

où a, b et c sont des constantes. Dans ce cas,

D = \{ (x,y) \in \mathbb{R}^2 \ | \ ax + by + c = 0 \}

Dans l'espace

Dans un espace à trois dimensions, l'ensemble des points 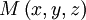M\left(x,y,z\right) formant D peut se représenter par un système de deux équations de la forme :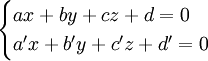 \begin{cases}ax+by+cz+d=0\\a'x+b'y+c'z+d'=0\end{cases}


où a, b, c, d, a', b', c', d' sont des constantes.

ax + by + cz + d = 0 et a'x + b'y + c'z + d' = 0 sont deux équations de plan.

Exemple

Dans le plan, la droite D passant par les points A( − 1,4) et B(1,0), a pour équation:

− 2x − y + 2 = 0.

Cas particuliers

Dans le plan, une droite D parallèle à l'axe des abscisses (horizontale) a une équation de la forme:

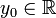
y = y0. avec y_0 \in \mathbb{R}

De même, une droite D parallèle à l'axe des ordonnées (verticale) a une équation de la forme:

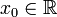
x = x0. avec x_0 \in \mathbb{R}

Recherche d'une équation de droite

1 ) Caractérisation d'une équation de droite : Soit l'équation à deux inconnues y = 3x - 2. Recherchez 5 couples solutions de cette équation. Représentez dans un repère les points associés.

Recherchons des solutions.

Il faut choisir une valeur pour x puis calculons la valeur de y correspondante. Par exemple : Si x = 0 alors y = 3 x 0 - 2 ; y = -2 Un couple solution est (0 ; -2)

Si x = 1 alors y = 3 x 1 - 2 ; y = 1 (1 ; 1) est solution de l'équation

Si x = 2 alors y = 3 x 2 - 2 ; y = 4 Je trouve la solution (2 ; 4).

Si x = -1 alors y = 3 x (-1) - 2 ; y = -5 Un couple solution est (-1 ; -5)

si x = 1/2 alors y = 3 x 1/2 - 2 = 3/2 - 4/2 ; y = -1/2. Un couple solution est (1/2 ; -1/2)


Représentons dans un repère (O,I,J) ces solutions sur un graphique en associant à chacun de ces couples un point qui a les mêmes coordonnées.

Tous les points sont alignés.

L' équation à deux inconnues y = 3x - 2 est une équation de droite.

Le nombre 3 représente la pente de la droite. C'est le coefficient directeur.

Le nombre -2 représente l'ordonnée du point d'abscisse 0, intersection de la droite avec l'axe des ordonnées. C'est l'ordonnée à l'origine.

Par résolution d'un système d'équations

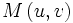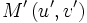Soient deux points non confondus du plan, M\left(u,v\right) et M'\left(u',v'\right).

Si la droite passant par ces deux points n'est pas verticale (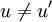u\not=u'), son équation est y = ax + b.

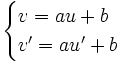
Pour trouver son équation, il faut résoudre le système : \begin{cases}v=au+b \\v'=au'+b\end{cases}

On a 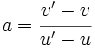a=\cfrac{v'-v}{u'-u} (coefficient directeur).

Pour trouver la constante b (ordonnée à l'origine), il suffit de remplacer les variables x et y respectivement par u et v (ou u' et v').

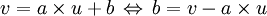On a alors v=a\times u+b\, \Leftrightarrow \, b=v-a\times u.

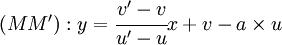
L'équation de la droite est alors au final \left(MM'\right):y=\cfrac{v'-v}{u'-u}x+v-a\times u

Par colinéarité de deux vecteurs

Soient A et B deux points non confondus du plan.

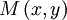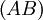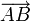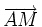M\left(x,y\right) est un point de la droite \left(AB\right) si et seulement si les vecteurs \overrightarrow{AB} et \overrightarrow{AM} sont colinéaires.

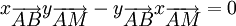On obtient l'équation de la droite en écrivant x_{\overrightarrow{AB}}y_{\overrightarrow{AM}}-y_{\overrightarrow{AB}}x_{\overrightarrow{AM}}=0.

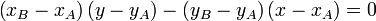C'est-à-dire \left(x_B-x_A\right)\left(y-y_A\right)-\left(y_B-y_A\right)\left(x-x_A\right)=0.

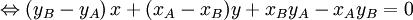
\Leftrightarrow \left(y_B-y_A\right)x+(x_A-x_B)y+x_By_A-x_Ay_B=0

Par orthogonalité de deux vecteurs

Soient A un point du plan et n un vecteur non nul.

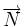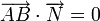La droite passant par A de vecteur normal \overrightarrow{N} est l'ensemble des points B du plan tel que \overrightarrow{AB}\cdot\overrightarrow{N}=0.

Remarques

  • Une droite peut avoir une infinité d'équations qui la représentent.
  • Dans le plan, toute droite admet une équation (dite cartésienne) de la forme : ax + by + c = 0.

Lien interne

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « %C3%89quation de droite ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation d'une droite de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Equation de droite — Équation de droite Sommaire 1 Définition 1.1 Dans le plan 1.2 Dans l espace 2 Exemple 3 Cas particulier …   Wikipédia en Français

  • Distance d'un point à une droite — La distance entre le point A et la droite (d ) est la distance AAh En géométrie euclidienne, la distance d un point à une droite est la plus courte distance séparant ce point et un point courant de la droite. Le théorème de Pythagore permet d… …   Wikipédia en Français

  • Equation normale — Équation normale Droite du plan Dans un plan affine euclidien, l équation d une droite affine ax + by + c = 0 est normale si et seulement si a2 + b2 = 1. a et b sont alors les cosinus directeurs de la normale N à la droite passant par l origine,… …   Wikipédia en Français

  • Équation normale — Droite du plan Dans un plan affine euclidien, l équation d une droite affine ax + by + c = 0 est normale si et seulement si a2 + b2 = 1. a et b sont alors les cosinus directeurs de la normale N à la droite passant par l origine, c est à dire que… …   Wikipédia en Français

  • droite — [ drwat ] n. f. • XVIe; de droit I ♦ (de 2. droit) 1 ♦ Le côté droit, l aile, la partie droite. Il ne sait pas distinguer sa droite de sa gauche (⇒ latéralisé) . La droite d un navire. ⇒ tribord. Se coucher sur la droite. Se diriger vers la… …   Encyclopédie Universelle

  • Équation de droite — Sommaire 1 Définition 1.1 Dans le plan 1.2 Dans l espace 2 Cas particuliers 3 …   Wikipédia en Français

  • Equation — Équation (mathématiques)  Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires).   …   Wikipédia en Français

  • Équation (mathématiques) —  Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires).   …   Wikipédia en Français

  • Équation symétrique — Équation (mathématiques)  Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires).   …   Wikipédia en Français

  • Équation vectorielle — Équation (mathématiques)  Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires).   …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”